Автоколебания в механических системах
уравнения Ван-дер-Поля
В качестве модели, описывающей автоколебания в радиотехническом генераторе, рассмотрим уравнение Ван-дер-Поля.
А это уравнение Ван-дер-Поля. Обыкновенное дифференциальное уравнение второго порядка с параметром \(\lambda\).
\( y'' + (\lambda - y'^2)y' + y = 0 \)
Для моделирования переходных процессов придётся свести данное уравнение к системе в нормальной форме. Введём новые переменные:
\begin{cases} z_1 = y \\ z_2=y' \end{cases}
Тогда в новых обозначениях, получим систему ОДУ 1-го порядка:
\begin{cases} z_1' = z_2 \\ z_2' = -z_1 + (z_2^2 - \lambda)z_2 \end{cases}
Найдём особые точки данной системы: то есть точки, в которых скорости нулевые:
\begin{cases} 0 = z_2 \\ 0 = -z_1 + (z_2^2 - \lambda)z_2 \end{cases} \begin{cases} 0 = z_2 \\ 0 = -z_1 \end{cases}
Итак, нашлась всего одна особая точка \( (z_1, z_2) = (0,0) \) , или в исходных обозначениях: \( y=y'=0 \).
Данная точка является:
- устойчивым узлом при \(\lambda < -2 \)
- устойчивым фокусом при \(-2 < \lambda < 0\)
- неустойчивым фокусом при \(0<\lambda<2\)
- неустойчивым узлом при \(\lambda>2\)
Кроме того, в данной системе наблюдается возникновение предельных циклов.
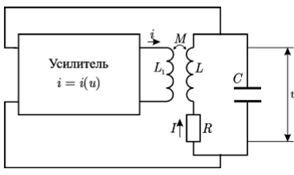
Рассмотрим, как меняется поведедение системы в зависимости от значений параметра \(\lambda\)
clc; clf;
//Функция, описывающая систему дифференциальных уравнений
function dz = syst(t, z, lam)
dz(1) = z(2);
dz(2) = -z(1) + (-z(2)*z(2) + lam)*z(2);
endfunction
//Решение системы дифференциальных уравнений
z0 = [1e-2; 1e-2];
t0 = 0;
t = 0:1e-2:50;
//Массив значений параметра
lam = [.1; 1.1; 10];
//Решаем три системы ОДУ с разными люмбда
z1 = ode(z0, t0, t, list(syst, lam(1)));
z2 = ode(z0, t0, t, list(syst, lam(2)));
z3 = ode(z0, t0, t, list(syst, lam(3)));
subplot(321);
plot(t, z1); xgrid(); xtitle("Автоколебания квазигармонические", "t", "x,y"); legend("x", "y");
subplot(322);
xgrid(); xtitle("Фазовая плоскость", "x", "y");
fx= min(z1(1,:)):0.01:max(z1(1,:));
fy= min(z1(2,:)):0.01:max(z1(2,:));
fchamp(list(syst, lam(1)), 0, fx, fy);
comet(z1(1,:), z1(2,:));
plot(z1(1,:), z1(2,:));
subplot(323);
plot(t, z2); xgrid(); xtitle("Автоколебания негармонические", "t", "x,y"); legend("x", "y");
subplot(324);
xgrid(); xtitle("Фазовая плоскость", "x", "y");
fx= min(z2(1,:)):0.1:max(z2(1,:));
fy= min(z2(2,:)):0.1:max(z2(2,:));
fchamp(list(syst, lam(2)), 0, fx, fy);
comet(z2(1,:), z2(2,:));
plot(z2(1,:), z2(2,:));
subplot(325);
plot(t, z3); xgrid(); xtitle("Авоколебания релаксационные", "t", "x,y"); legend("x", "y");
subplot(326);
xgrid(); xtitle("Фазовая плоскость", "x", "y");
fx= min(z3(1,:)):1:max(z3(1,:));
fy= min(z3(2,:)):1:max(z3(2,:));
fchamp(list(syst, lam(3)), 0, fx, fy);
comet(z3(1,:), z3(2,:));
plot(z3(1,:), z3(2,:));
Химические колебания. Брюсселятор
Для погружения в циклическую генерацию решений, мы рассмотрим простой модельный пример: гипотетическую химическую реакцию, которая получила название Брюсселятор . Уравнения этой реакции имеют вид:
\begin{cases} A \xrightarrow{k_1} X \\ B+x \xrightarrow{k_2} Y+D \\ 2X+Y \xrightarrow{k_3} 3X \\ X \xrightarrow{k_4} E \\ \end{cases}
Кинетические уравнения для данной системы будут иметь вид:
\begin{cases} \frac{dX}{dt} = k_1A - k_2BX + k_3X^2Y - k_4X \\ \frac{dY}{dt} = k_2BX + k_3X^2Y \end{cases}
Заведём новые переменные, чтобы не перегружать систему параметрами:
\begin{cases} \tau = kt \\ x = \sqrt{\frac{k_3}{k_4}}X \\ y = \sqrt{\frac{k_3}{k_4}}Y \\ z_1 = x\\ z_2 = y \end{cases}
Тогда кинетические уравнения преобразуются к виду:
\begin{cases} z_1' = a - (b+1)z_1 + z_1^2z_2 \\ z_2' = bz_1 - z_1^2z_2 \end{cases}
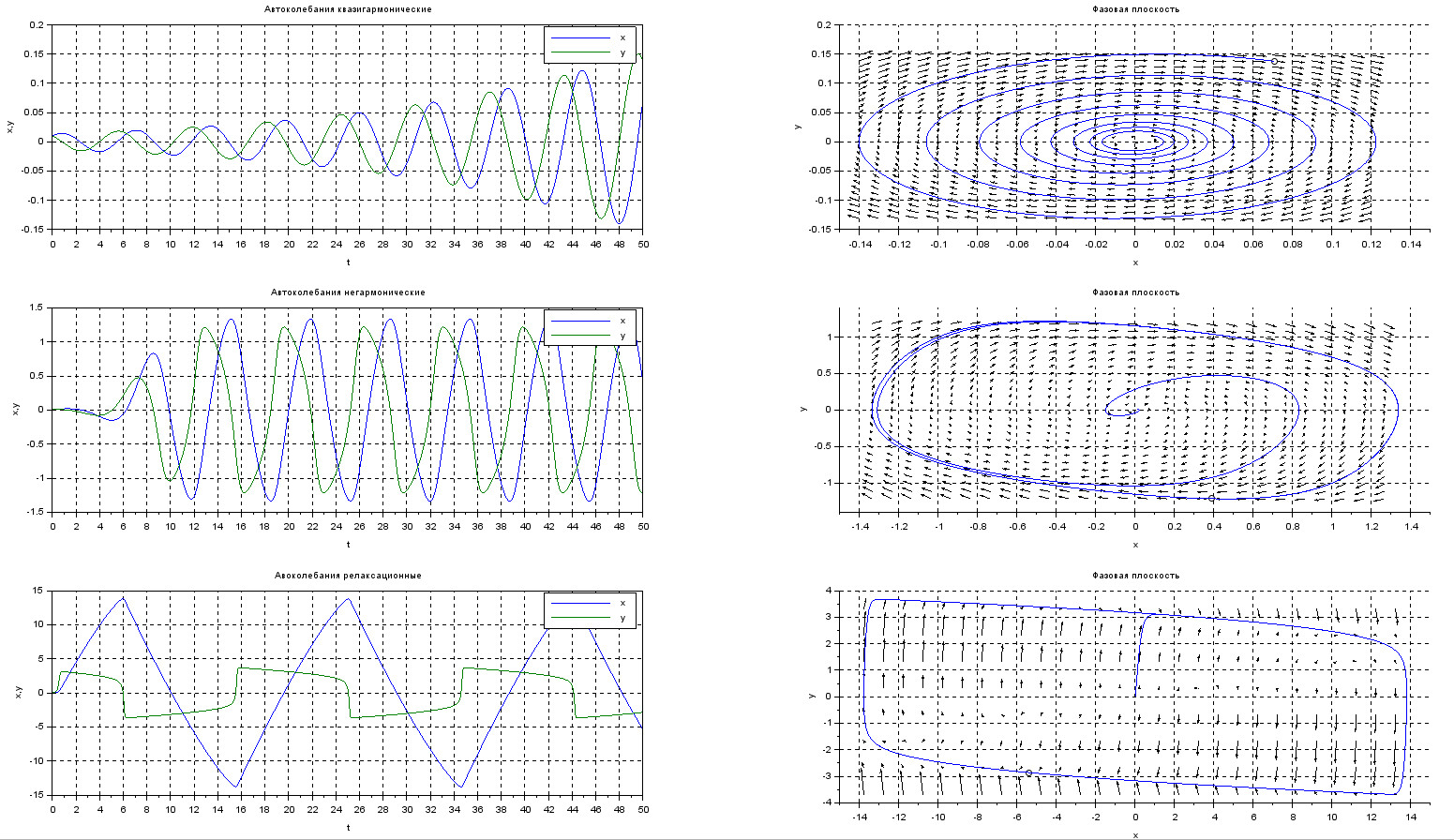
Замоделируем поведение решений системы ОДУ с различными параметрами и начальными условиями.
Приведённый ниже код включает в себя несколько примеров, рассмотренных ранее: использование циклов, обращение к графикам на координатной сетке, как к потомкам объекта axes, а также, задание цвета в формате rgb, где значения каждого из параметров генерируются случайным образом.
clc; clf;
//Функция для генерации случайного значения из заданного промежутка
function rnd = randomRange(a,b)
rnd = a + (b-a) * rand()
endfunction
//Функция, описывающая систему дифференциальных уравнений
function dz = syst(t, z, aa, bb)
dz(1) = aa -( bb + 1 )*z(1) + z(1)*z(1)*z(2);
dz(2) = bb*z(1) - z(1)*z(1)*z(2);
endfunction
//зададим пары случайных начальных условий
z_0 = [0 0.5; 0 1.5; 2.5 0.01; 0.5 3; 1 0; 1 1; 1.5 1.2; 2 2; 0.5 2.1]'
z_length = size(z_0)
t0 = 0; //начальный момент времени
t = 0:1e-2:20; //отрезок интегрироваония
a = 1; // первый параметр
b = [.85; 3.0; 5]; //три варианта параметра b
n = length(b)
for i = 1:n
subplot(1,n,i);
xgrid();
str = 'Брюсцелятор с параметрами: a=' + string(a) + ', b=' + string(b(i));
xtitle(str, "z1", "z2");
axe = get("current_axes")
axe.font_size = 3;
axe.data_bounds = [-.5,-.5; 3.5,3.5];
for j = 1:z_length(2)
z_0_cur = z_0(:, j);
z = ode(z_0_cur, t0, t, list(syst, a, b(i)));
plot(z(1,:), z(2,:));
axe.children.children(1).foreground = color(randomRange(0,255),randomRange(0,255),randomRange(0,255));
axe.children.children(1).thickness = 2;
end
end

Комментарии