Решение дифференциальных уравнений в Scilab
Дифференциальные уравнения возникают в широком классе задач по описанию управляемых энергетических, промышленных и других процессов и комплексов. В настоящее время наблюдается бурное развитие робототехники, разработка и эксплуатация новых моделей роботов и промышленных манипуляторов, что стимулирует активные исследования по математической и прикладной теории управления, моделированию и конструированию управляемых систем.
Мы рассмотрим способы исследования сложных механических систем, моделируемых дифференциальными уравнениями. Рассмотрим способы конструирования управления нескольких видов для механической системы с двумя степенями свободы. А также, проведем визуализацию процесса стабилизации движения.
Дифференциальные уравнения n-го порядка
Дифференциальным уравнением n-го порядка называется соотношение вида
\( H(t, x', x'', ... ,x^{(n)}) =0 \)
Решением дифференциального уравнения является функция \( x(t) \), которая обращает это уравнение в тождество. Дифференциальные уравнения имеют бесконечное множество решений.
Чтобы однозначно определить решение некоторой задачи, необходимо задавать начальные условия. Количество таких условий должно совпадать с порядком уравнения. А решение, найденное для таких условий называется решением задачи Коши.
6.2 Пример решения оду в Scilab
Для решения обыкновенных дифференциальных уравнений (ОДУ) в Scilab используется
функция y = ode([type], y0, t0, t, func).
Разберём, что обозначает каждый из параметров у этой функции.
type - необязательный строковый параметр, с помощью которого можно выбрать метод решения ОДУ. Обычно этот параметр опускается.
t0 - скаляр начальный момент отрезка интегрирования. Обычно \( t0 = 0 \).
y0 - начальные условия. Отметим, что \(y0 \) это вектор, размерность которого совпадает с порядком ОДУ. Так, для ОДУ 2-го порядка необходимо задать значения в начальный момент времени для функции и её производной, т.е. использовать запись \(y0 = [0.1, 0.3]\).
t - вектор, задающий узлы сетки, в которых ищем решение. Как правило, вектор t задается следующим образом t=t0:d:tmax, где \(t0\) - начальный момент отрезка интегрирования, \(d\) - шаг дискретизации, \(tmax\) - конечный момент отрезка интегрирования.
func - пользовательская функция, определяющая правую часть уравнения.
y - вектор решений.
Рассмотрим использование функции ode() на примере решения следующей задачи.
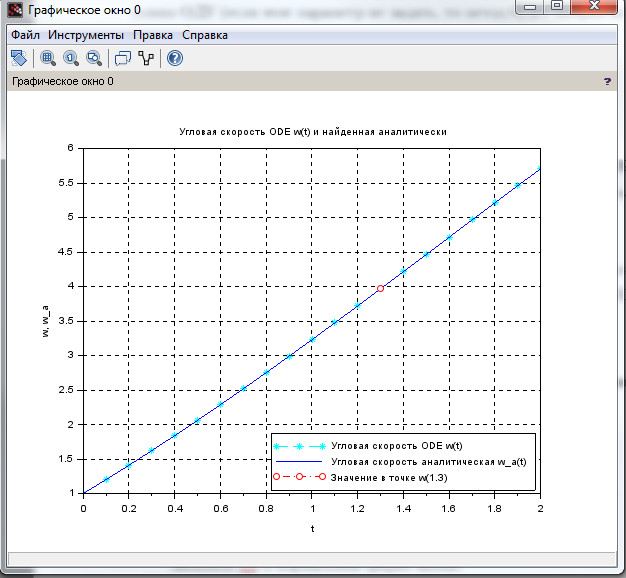
Найти угловую скорость \( \omega(t) \) твердого тела вокруг неподвижной оси, если заданы начальная угловая скорость тела \( \omega_0=1 \) и угловое ускорение \( \varepsilon(t) = 2+0.5sin(t) \). Найти значение \( \omega(t) \) в момент времени \( t_1=1.3 \). Построить график функций.
Угловая скорость точки может быть найдена из дифференциального уравнения
\( \omega = {d\varphi \over dt} \)
В нашем случае по условию задачи указаны следующие параметры для функции ode():
\(t0=0 \) начальный момент времени,
\(y0 = 1\) начальное условие одно, т.к. порядок уравнения равен 1, это начальная угловая скорость тела \( \omega_0=1 \)
t=t0:h:tmax - вектор, задающий узлы сетки.
Результат работы программы представлен на рис.9, исходный код на листинге 15.
clf;
// аналитически найденная функция omega
function f = aomega(t)
f = 2*t-0.5*cos(t)+omega0+0.5
endfunction
//функция epsilon из условия задачи
function f=epsilon(t)
f = 2+0.5*sin(t)
endfunction
//функция решения ОДУ
function dx = syst(t,x)
dx = epsilon(t);
endfunction
t0 = 0; // начало отрезка интегрирования
tmax = 2; // конец отрезка интегрирования
h=0.1 // шаг дискретизации
T=t0:h:tmax; // вектор, задающий узлы сетки
omega0 = 1; // начальное условие
ts = 1.3; // точка, в которой нужно вычислить значение
omega = ode(omega0, t0, T, syst);
plot(T, omega, '*cya--');
plot(T, aomega(T));
plot(ts, aomega(ts), 'ro-.');
xtitle('Угловая скорость ODE w(t) и найденная аналитически', 't', 'w, w_a');
legend('Угловая скорость ODE w(t)','Угловая скорость аналитическая w_а(t)','Значение в точке w(1.3)', 4,%t); xgrid();
Отметим, что в данной программе фигурирует пользовательская функция aomega(t), представляющая собой угловую скорость, найденную аналитически с указанным начальным условием.
Функция \( f = 2t - 0,5cos(t) + 1,5 \) единственное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям, то есть, функция \(f\) решение задачи Коши.
6.3 Cистемы дифференциальных уравнений
Для решения систем ОДУ в Scilab используется та же функция y = ode([type], y0, t0, t, func). Однако важным требованием является запись исследуемой системы в нормальной форме Коши.
Системой дифференциальных уравнений, записанной в нормальной форме Коши называется система, где слева стоят производные фазовых переменных, а справа некоторые функции, т.е. система вида
\begin{cases} x_1' = f_1(t,x_1,...x_n) \\ x_2' = f_2(t,x_1,...x_n) \\ ...\\ x_n' = f_n(t,x_1,...x_n) \end{cases}
Решением системы ОДУ является вектор x(t), который обращает это уравнение в тождество. Размерность вектора равна количеству уравнений в системе.
Стоит отметить, что дифференциальное уравнение n-ой степени может быть представлено в виде системы из n-уравнений первой степени, что позволяет решать задачу Коши для полученной системы ОДУ.
6.4 Примеры поиска решения систем ОДУ в Scilab
Решение системы ОДУ
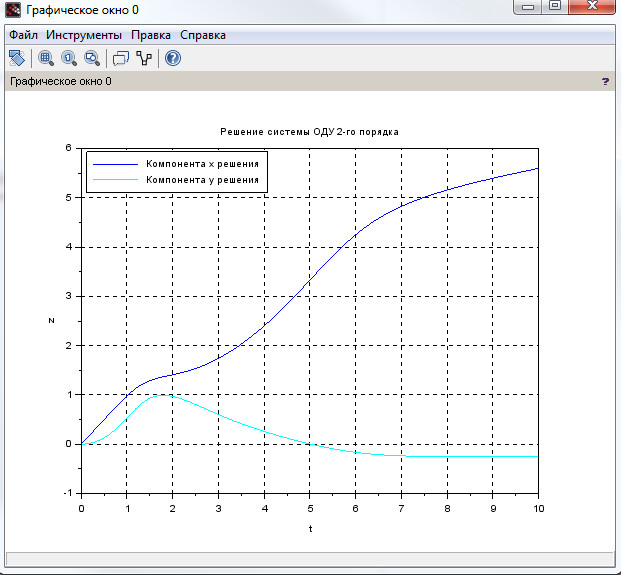
Рассмотрим решение задачи Коши для системы уравнений
\begin{cases} x' = cos(xy) \\ y' = sin(x+ty) \end{cases}
на интервале \( [0; 10]\) и с начальными условиями \(x(0)=0, y(0)=0 \).
Для поиска решения данной задачи, нам необходимо привести исходную систему к нормальному виду Коши. Для этого введём новые переменные \( (z1, z2) \) и сделаем необходимые переобозначения в исходной системе:
Рассмотрим решение задачи Коши для системы уравнений
\begin{cases} z_1 = x \\ z_2 = y \end{cases} \begin{cases} z_1' = cos(z_1 z_2) \\ z_2' = sin(z_1 + t z_2) \end{cases}
Код программы, реализующей поиск решения системы дифференциальных уравнений представлен на листинге 16. Обратите внимание, как происходит обращение к компонентам вектора решения \( z(t) \).
clc;
//Функция, описывающая правую часть OДУ
function dz = syst(t,z)
dz = zeros(2,1);
dz(1) = cos(z(1)*z(2));
dz(2) = sin(z(1)+z(2)*t);
endfunction
//Начальтные условия
t0 = 0; tmax = 10; x0 = [0;0]; t= t0:0.1:tmax;
z = ode(x0, t0, t, syst);
plot(t, z(1,:));
plot(t, z(2,:), "c-");
xtitle('Решение системы ОДУ 2-го порядка', 't', 'z');
legend('Компонента x решения','Компонента y решения', 2,%t); xgrid();
Для наглядной реализации сформировано графическое решение на рис. 10.
Решение системы ОДУ в матричной форме
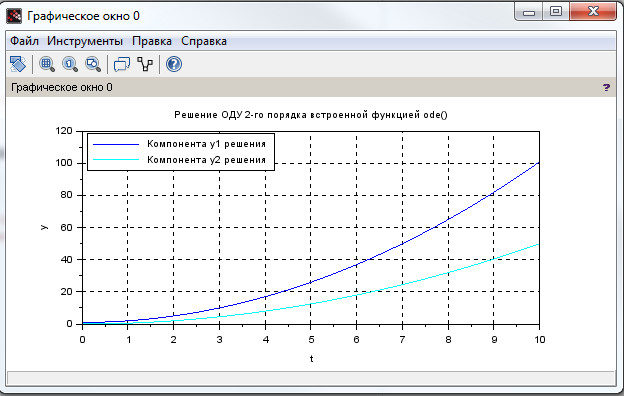
Рассмотрим решение задачи Коши для системы уравнений, заданных в матричном виде
\begin{matrix} {dy \over dx} =Ax, & y= { \Biggl( \begin{matrix} y_1 \\ y_2 \end{matrix} \Biggr) }, & A= { \Biggl( \begin{matrix} 2 & 0 \\ 1 & -1 \end{matrix} \Biggr) } \end{matrix}
на интервале \( [0; 10] \) и начальными условиями \( y_1(0)=1, y_2(0)=0 \).
Код программы, реализующей поиск решения системы дифференциальных уравнений представлен на листинге 17. Обратите внимание, как происходит обращение к компонентам вектора решения \(y(t)\).
clc;clf();
//Функция, описывающая правую часть ОДУ
function dy = syst(x, y, A)
dy = A*x;
endfunction
A = [2,0;1,-1];
//Начальтные условия
t0 = 0; tmax = 10; t= t0:0.1:tmax;
y0 = [1; 0];
y = ode(y0, t0, t, list(syst, A));
plot(t, y(1,:));
plot(t, y(2,:), "c-");
xtitle('Решение ОДУ 2-го порядка встроенной функцией ode()', 't', 'y');
legend('Компонента y1 решения','Компонента y2 решения', 2,%t); xgrid();
Для наглядной реализации сформировано графическое решение на рис. 11.
Решение ДУ 2-го порядка путём сведения к системе уравнений
Продолжим знакомиться с возможностями функции ode() на примере решения задачи механики на второй закон Ньютона.
Груз находится на пружине жёсткости \( c=12 \) H/м, масса груза \( m=68.7 \) кг. Определить закон движения груза, если на него действует сила \( F=100.5sin(2t) + {2\pi \over 3} \) H.
По 2-му закону Ньютона, движение груза описывается с помощью дифференциального уравнения 2-й степени, которое имеет вид:
\( \ddot{mx} =-cx + F(t) \)
и начальными условиями \( x(0)= 0, ;\ \dot{x}(0)= 0 \).
Как известно, ОДУ второго порядка сводится к системе в нормальной форме Коши, состоящей из двух уравнений первой степени. Введём новые переменные \( (z_1, z_2) \) и сделаем необходимые переобозначения в исходной системе:
\begin{cases} z_1 = x \\ z_2 = \dot{x} \end{cases} \begin{cases} \dot{z}_1 = z_2 \\ \dot{z}_2 = {1 \over m}(-cz_1 + F(t)) \end{cases}
Код программы, реализующей поиск решения системы дифференциальных уравнений представлен на листинге 18. Обратите внимание, как происходит обращение к компонентам вектора решения \( y(t) \).
clc;clf();
//Функция, действующая на груз F
function f = F(t)
f = 100.5*sin(2*t) + 2*%pi/3;
endfunction
//Функция, описывающая правую часть СДУ
function dz = syst(t, z, m, c)
dz = zeros(2,1);
dz(1) = z(2);
dz(2) = ( 1/m )*( -c*z(1) + F(t) );
endfunction
m = 68.7; // масса груза
c = 12; // Жёсткость пружины
//Начальтные условия
t0 = 0; tmax = 20; t= t0:0.01:tmax;
z0 = [0; 0];
z = ode(y0, t0, t, list(syst, m, c));
subplot(211);
plot(t, z(1,:));
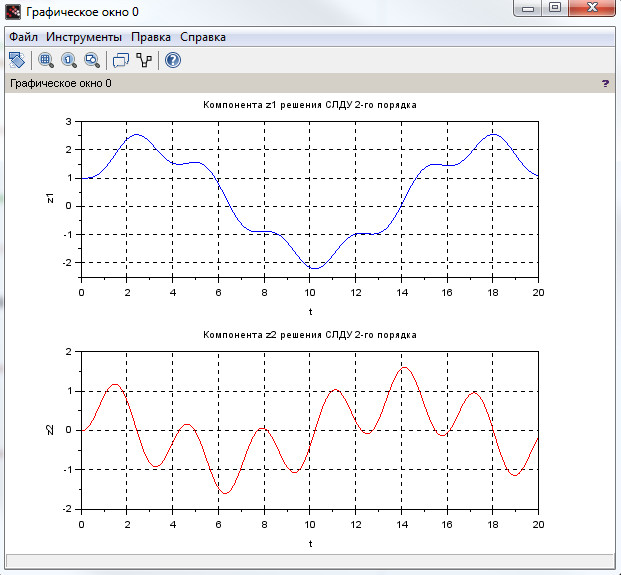
xtitle('Компонента z1 решения СЛДУ 2-го порядка', 't', 'z1');
xgrid();
subplot(212);
plot(t, z(2,:), "r-");
xtitle('Компонента z2 решения СЛДУ 2-го порядка', 't', 'z2');
xgrid();
Для наглядной реализации сформировано графическое решение на рис. 12. Компонента \( z_1 \) представляет собой координату груза, а компонента \( z_2 \) - скорость груза.

Комментарии