Основные операторы языка Scilab
Часто в процессе решения инженерных или физических задача, а также задач по математическому моделированию, возникает необходимость проверять корректность полученных данных, выполнять разные вычисления, в зависимости от полученных результатов, перебирать значения и т.д. Для этих нужд в Scilab существуют операторы цикла, присваивания, условные операторы, как и в других языках программирования.
Рассмотрим основные операторы, которые используются в процессе программирования в математическом пакете Scilab.
4.1 Операторы цикла for и while
Оператор цикла for
Оператор цикла for состоит из заголовка, содержащего условия его выполнения, исполняемого тела цикла. Форма записи представлена ниже:
for j = jo:d:jmax
операторы
end;
Здесь \( jo \) – это стартовое значение параметра,
\( d \) – значение, на которое увеличивается параметр \( j \) на каждом шаге \( j = j+d \),
\( jmax \) – конечное значение параметра \( j \).
Выполнение цикла начинается с присвоения параметру \( j \) начального значения \( jo \). Если параметр удовлетворяет условию \( j \le jmax \),то выполняются операторы тела цикла. Затем параметр \( j \) увеличивается на величину \( d \), и снова происходит проверка на выполнение условия \( j \le jmax \).
Оператор заканчивает свою работу, как только значение \( j \) превышает \( jmax \), а управление передаётся следующим за телом цикла операторам.
В качестве примера использования оператора for , рассмотрим метод Рунге-Кутты численного интегрирования обыкновенного дифференциального уравнения.
Рассмотри дифференциальное уравнение
\( y'=f(x,y) \)
с начальным условием \( y(x_0)=y_0 \). Положим \( f(x,y)=sin(x)\).
Классический метод Рунге-Кутты 4-го порядка описывается следующей системой
\( y_{i+1} = y_i + {h\over6}(k_1 + 2k_2 + 2k_3+k_4) \)
где
\( k_1 = f(x_i, y_i) \)
\( k_2 = f(x_i+ {h\over2}, y_i+ {h\over2}k_1) \)
\( k_3 = f(x_i+ {h\over2}, y_i+ {h\over2}k_2) \)
\( k_4 = f(x_i+ h, y_i+ hk_3) \)
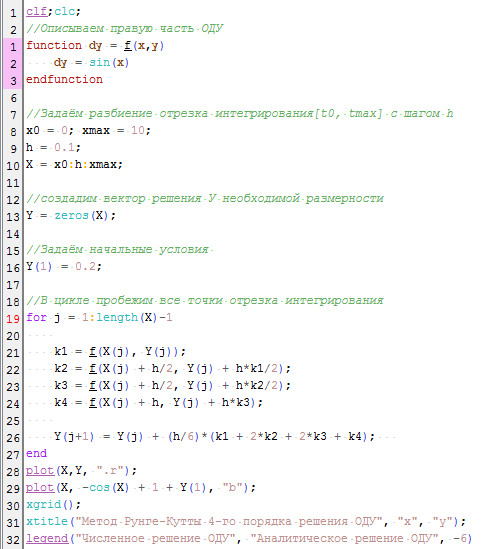
Таким образом, для нахождения численного решения дифференциального уравнения \( y' = sin(x) \) с иcпользованием метода Рунге-Кутты 4-го порядка, нам потребуется написать пользовательскую функцию (Листинг 10, строки 2-5), описывающую правую часть ОДУ.
Далее, задать отрезок интегрирования с некоторым шагом h, что соответствует строкам 7-10 Листинга 10. Заострим внимание читателя на том, что на строке 10 Листинга 10 мы сформировали строку из 101 элемента, а на строке 13 Листинга 10 -- вектор той же размерности. Обратите внимание, как задаются начальные условия (Листинг 10, строка 16).
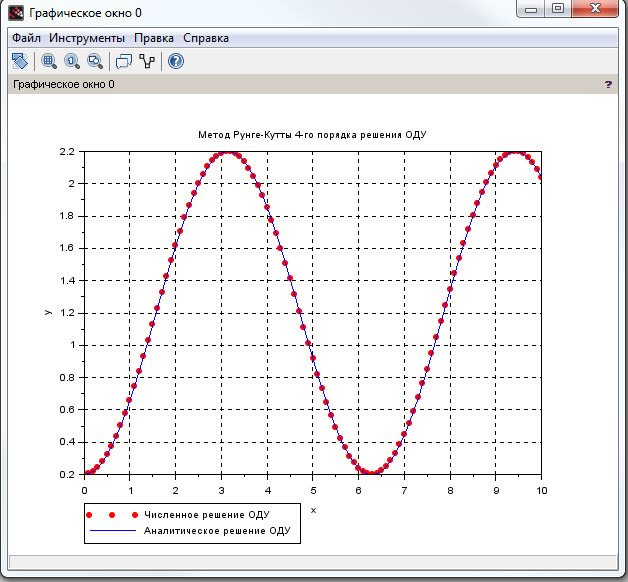
Строки 19 – 27 Листинга 10 соответствуют реализации метода Рунге-Кутта, описанного выше. Результатом работы приложения будут графики решений ОДУ , полученных численно и аналитически (см. рис. 6).
clf;clc;
//Описываем правую часть ОДУ
function dy = f(x,y)
dy = sin(x)
endfunction
//Задаём разбиение отрезка интегрирования[t0, tmax] с шагом h
x0 = 0; xmax = 10;
h = 0.1;
X = x0:h:xmax;
//создадим вектор решения У необходимой размерности
Y = zeros(X);
//Задаём начальные условия
Y(1) = 0.2;
//В цикле пробежим все точки отрезка интегрирования
for j = 1:length(X)-1
k1 = f(X(j), Y(j));
k2 = f(X(j) + h/2, Y(j) + h*k1/2);
k3 = f(X(j) + h/2, Y(j) + h*k2/2);
k4 = f(X(j) + h, Y(j) + h*k3);
Y(j+1) = Y(j) + (h/6)*(k1 + 2*k2 + 2*k3 + k4);
end
plot(X,Y, ".r");
plot(X, -cos(X) + 1 + Y(1), "b");
xgrid();
xtitle("Метод Рунге-Кутты 4-го порядка решения ОДУ", "x", "y");
legend("Численное решение ОДУ", "Аналитическое решение ОДУ", -6)
Оператор цикла while
Оператор цикла while состоит из заголовка, содержащего условия его выполнения, исполняемого тела цикла. Форма записи представлена ниже:
while условие
операторы
end;
Выполнение цикла начинается с проверки условия на истинность. Если условие истинно, то выполняются операторы тела цикла. Затем снова происходит проверка на истинность условия.
Оператор заканчивает свою работу, как только значение условие нарушается, а управление передаётся следующим за телом цикла операторам.
Приведём пример использования данного оператора. Попросим пользователя ввести радиус \( R=5\). При этом, если пользователь введёт число, не превосходящее 5, условие прекращения цикла не будет выполнено и запрос на ввод радиуса повторится. При вводе корректного значения в консоли, мы выводим его в командном окне (строка 8) и присваиваем переменной R введённое пользователем значение (см. листинг 11).
/* Работа цикла while */
R=0;
while (R < 5)
clc;
R = input('Введите радиус R больше 5');
end;
disp("R=");
disp(R);
4.2 Условный оператор if
Для проверки выполнения каких-либо условий в программе используется условный оператор if. Это один из основных операторов языка, и он имеет две формы записи: обычную и расширенную.
Обычная форма записи позволяет выбрать одно из двух условий и выполнить соответствующие действия.
if условие then
операторы 1
else
операторы 2
end;
Расширенная форма записи позволяет работать с конечным числом условий и выполнять соответствующие корректному условию операторы. В данном случае, поочередно проверяются все условия от 1 до n-го. Если ни одно из условий не выполнилось, выполняются операторы по ветке else.
if условие1 then
операторы 1
elseif условие2
операторы 2
elseif условие3
операторы 3
else
операторы
end;
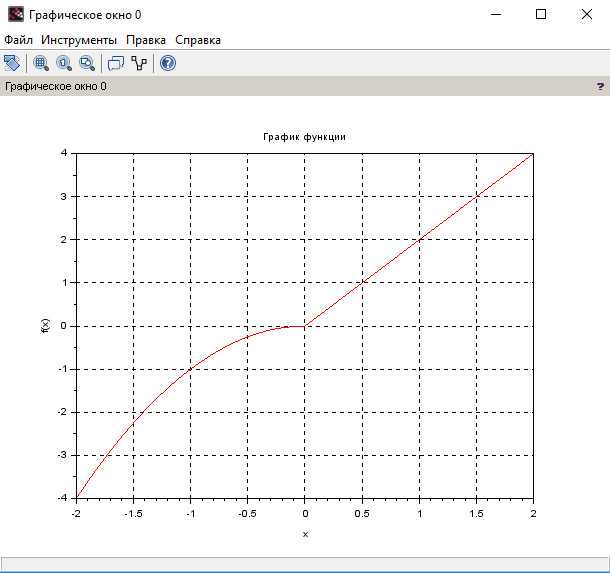
В качестве примера, напишем пользовательскую функцию, которая будет вычислять значения функции \( f(x) = \begin{cases} 2x, & x>0 \\ -x^2, & \text{иначе} \end{cases} \) на промежутке \( [-2; 2] \) с шагом \( d=0.1 \) (листинг 12). В данном случае в функцию myfunc() передаются два входных параметра: массив точек абсцисс \( Х \) и шаг \( d \).
В теле пользовательской функции на строке 2 вычисляется длина массива, а на следующей строке, функцией zeros(), создаётся массив нулевых элементов совместного размера для записи значений функции.
Далее, внутри цикла for производится перебор всех элементов входного массива \(х\), а условный оператор if передаёт управление операторам вычисления значения функции в точке \( x(j) \) , в зависимости от выполнения условия положительности или неотрицательности \(j-го \) элемента.
/* Использование опертора if */
clc; clf;
function z = myfunc(x, d)
el = length(x);
z = zeros(el);
for j = 1:1:el
if (x(j) > 0) then
z(j) = 2*x(j)
else
z(j) = -x(j)^2
end
end;
endfunction;
d = 0.1; // задаём шаг
X = -2:d:2; // задаём промежуток для переменной x
Y = myfunc(X, d); // вызываем пользовательскую функцию myfunc
plot(X,Y, "r");
plot(zeros(X), Y, "k");
plot(X, zeros(Y), "k");
xgrid;

Комментарии