Настройка линейного классификатора Scilab
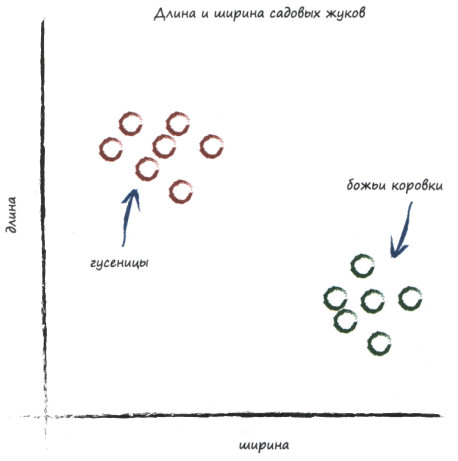
Рассмотрим задачу классификации данных на примере разделения садовых жуков.
Будем рассматривать гусениц и божьих коровок, разделяя их в зависимости от размера.
Определим шкалу, где по вертикали будет откладываться длина жука, а по горизонтали ширина.
Тогда на введённой шкале всех жуков можно условно разделить следующим образом:
Попробуем разделить наших жуков с помощью прямой. Уравнение прямой имеет вид:
\( y = Ax, \)
где A это коэффициент наклона.
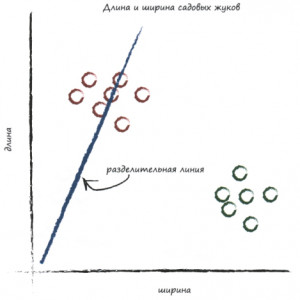
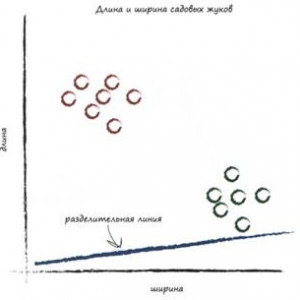
Проведём пару разделительных линий:
|
|
| Тут мы попали в гусениц. То, что выше линии гусеницы, то, что ниже линии - гусеницы и божьи коровки. Плохо разделили 🤨 | Тут мы ни в кого не попали, однако, выше линии оказались и гусеницы, и божьи коровки, а снизу никого. Совсем не разделили жуков 🤔 |
Итак, нам надо подобрать коэффициент наклона прямой таким образом, чтобы снизу были божьи коровки, а сверху - гусеницы:
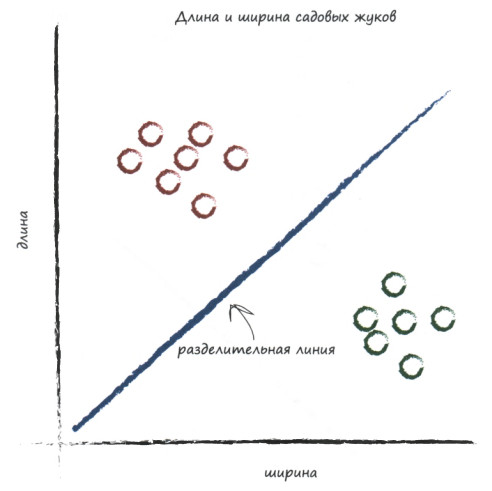
Тогда, выбирая некоторого жука на анализ, по его координатам (длине и ширине), мы поймём, где, относительно разделителя, он находится, а значит, сможем сказать, божья коровка это или гусеница.
Вот как-то, как на графике:
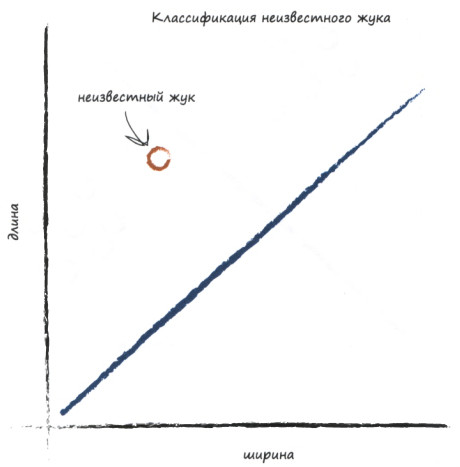
Тренировочные данные
Сейчас мы займемся тренировкой (обучением) нашего линейного классификатора и научим его правильно классифицировать жуков, относя их к гусеницам или божьим коровкам.
Первое, что нам понадобится - это эталонные данные, на основе которых мы будет тренировать классификатор.
Чтобы не усложнять себе жизнь, мы ограничимся двумя простыми примерами, приведенными ниже.
| Пример | Ширина | Длина | Жук |
|---|---|---|---|
| 1 | 3.0 | 1.0 | Божья коровка |
| 2 | 1.0 | 3.0 | Гусеница |
Итак, для обучения классификатора у нас в арсенале имеются:
- жук, имеющий ширину 3.0 и длину 1.0, который, как нам известно, является божьей коровкой;
- жук, имеющий ширину 1.0 и длину 3.0, которым является гусеницей.
Изобразим их на нашей шкале:
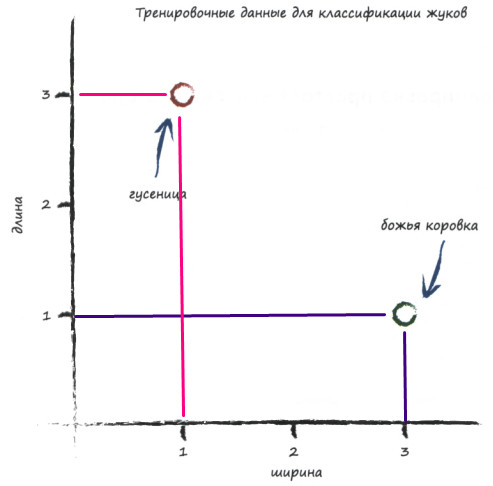
И попробуем построить классификатор. То есть, провести прямую \( y=Ax \) с некоторым коэффициентом наклона \( A \).
Возьмём \( А=0.25\). Тогда уравнение прямой будет иметь вид \( y=0.25x\). Изобразим наш классификатор на графике с жуками и посмотрим, каких результатов мы достигли:
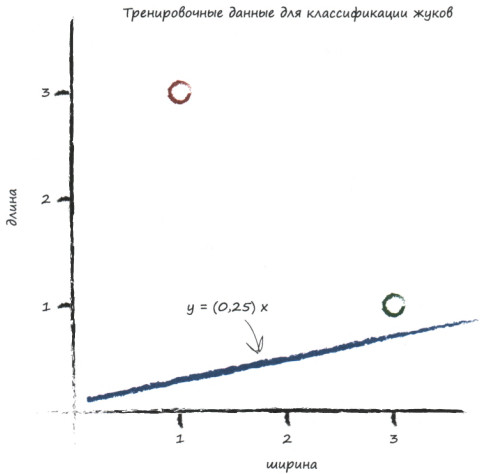
Так себе классификатор, честно говоря.
С таким классификатором мы не можем делать выводы вида: «Если точка данных располагается над линией, то она соответствует гусенице».
А именно к этому мы и стремимся: по графику понять, что за жук перед нами. Если он выше прямой - гусеница, ниже - коровка.
Процесс настройки классификатора
Приступим к выработке алгоритма, который бы подбирал оптимальный коэффициент наклона прямой.
Шаг 1
Возьмём первого эталонного жука - божью коровку: у неё ширина 3 (это х), длина 1 (это у). Подставим ширину жука в наш классификатор:
\( y = 0.25 \cdot 3 = 0.75 \)
Получили \(у=0.75 \), а по эталону должно было получиться \( y_э = 1 \). Налицо отклонение от эталона.
Шаг 2
Считаем ошибку которая вычисляется, как разница между желаемым значением и фактическим результатом.
\(e = y_э - y = 1 - 0.75 = 0.25 \)
Давайте подумаем, каким должно быть подходящее желаемое значение \( y \).
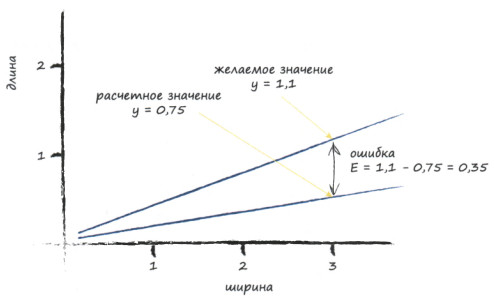
Если положить его равным 1, как в эталоне, то линия пройдет через точку с координатами (х, у) = (3; 1), соответствующую божьей коровке. Само по себе это неплохо, но это не совсем то, что нам нужно.
Нам желательно, чтобы линия проходила над этой точкой. Почему? Да потому, что мы хотим, чтобы точки данных божьей коровки лежали под линией, а не нанизывались на неё.
Поэтому, мы немного приподнимем классификатор, т.е.
отступим от \( y_э = 1 \) на небольшое значение \( D=0.1\)
Тогда ошибка будет вычисляться следующим образом:
\(e = y_э - y = 1.1 - 0.75 = 0.35 \)
На графике наши манипуляции с углом наклона прямой будут выглядеть так:
Шаг 3
Выясним как связаны \(A\) и \(D\).
Так как брать величину поправки с потолка нехорошо, формализуем поиск этого самого \(D\) - величины, на которую мы хотим изменить наклон классификатора.
Изначально классификатор имел уравнение
\(y=Ax \)
Приподняв его, мы произвели изменение угла наклона, получив прямую
\(y=(A+D)x \)
А теперь подставим эти данные в ошибку \( e \):
\(e = y_э - y = (A + D)x - Aх = Aх + Dx - Ax = Dx. \)
Итак, ошибка \( e \) связана с \( D \) очень простым соотношением. Используем информацию об ошибку для определения величины поправки \( D \):
\( D = \frac{e}{x} \)
Теперь мы можем использовать ошибку \( e \) для вычисления величины, на которую следует изменить наклон классификатора. В нашем случае:
\( D = \frac{0.35}{3}=0.1167 \)
Шаг 4
Корректируем наклон классификатора. Текущее значение \(А=0.25\) необходимо изменить на величину \( D = 0.1167 \), стало быть, улучшенное уравнение классификатора примет вид:
\( y = (0.25+0.1167)x=0.3667x \)
Итак, новый классификатор \( у=0,3667х \) получен на основе всего одного эталонного значения.
Проделаем те же манипуляции для второго жука, но уже с подстроенным классификатором \( у=0,3667х \).
Шаг 1
Подставим гусеницу \( (x,y) = (1, 3) \) в классификатор:
\( y = 0.3667 \cdot 1 = 0.3667 \)
Шаг 2
Посмотрим на эталон:
\( y_э = 3 \)
Отступим от эталона на \(D=0.1\) и посчитаем ошибку:
\(e = 2.9 - 0.3667 = 2.5333 \)
Шаг 3
Вычислим величину \( D \), на которую нужно изменить наклон классификатора: .
\( D = \frac{2.5333}{1}=2.5333 \)
Шаг 4
Корректируем наклон классификатора:
\( y = (0.3667 + 2.5333)x=2,9x \)
Отобразим на графике проделанные манипуляции:
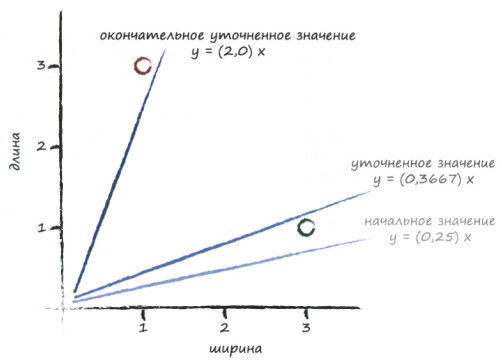
Глядя на график, мы видим, что нам не удалось добиться того наклона прямой, которого мы хотели.
Линия обновляется каждый раз, подстраиваясь под то целевое значение у, которое мы задаем. В результате этого мы отбрасываем весь предыдущий опыт обучения, который могли бы использовать, и учимся лишь на самом последнем примере.
Давайте это исправим.
Сглаживание поправки
Воспользуемся идеей, которая играет ключевую роль в машинном обучении.
Вместо того чтобы каждый раз с энтузиазмом заменять \(А \) новым значением, мы используем лишь некоторую долю поправки \(D \) , а не всю ее целиком.
Ну что ж, сделаем перерасчет шагов 1-3 для обоих жуков, на этот раз добавив сглаживание в формулу обновления коэффициента наклона:
\( D = L \frac{e}{х} \)
Фактор сглаживания, обозначенный здесь как \( L\), часто называют коэффициентом скорости обучения.
Выберем \( L=0,5 \) в качестве разумного начального приближения. Это означает, что мы собираемся использовать поправку вдвое меньшей величины, чем без сглаживания.
Повторим шаги 1-4 для обоих жуков, используя начальное значение \( А=0,25 \).
Тестирование божьей коровки \( (x,y) = (3, 1) \) дает нам:
- Вычисленное значение
\(у = 0.25 \cdot 3 = 0.75 \)
При целевом значении \(y_э = 1.1 \) ошибка \( e = 0.35 \)
- Поправка равна
\( D = L \frac{e}{х} = 0.5 \frac{0,35}{3} = 0.0583 \)
- Обновленное значение
\( А = 0.25 + 0.0583 = 0.3083 \)
В итоге на первом жуке уравнение прямой преобразуется к виду
\( y = 0.3083x\)
Проведём расчеты с новым значением \( А \) для гусеницы \( (x,y) = (1, 3) \).
- Вычисленное значение
\(у = 0.3083 \cdot 1 = 0.3083 \)
При целевом значении \(y_э = 2.9 \) ошибка \( e = 2.9 - 0.3083 = 2.5917 \)
- Поправка равна
\( D = L \frac{e}{х} = 0.5 \frac{2.5917}{1} = 1.2958 \)
- Теперь обновленное значение
\( А = 0.3083 + 1.2958 = 1.6042 \)
В итоге на втором жуке уравнение прямой преобразуется к виду
\( y = 1.6042x\)
Отобразим на графике начальный, улучшенный и окончательный варианты классификатора, чтобы убедиться в том, что сглаживание обновлений приводит к более удовлетворительному расположению разделительной линии между областями данных божьих коровок и гусениц:
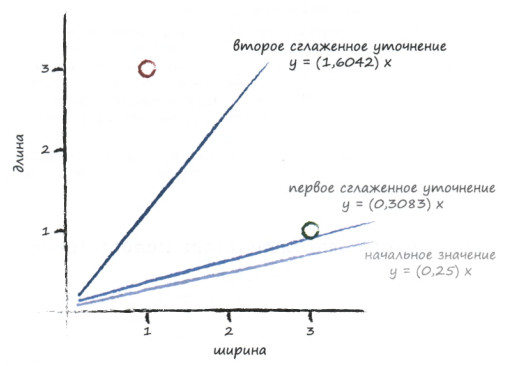
Это действительно отличный результат!
Всего лишь с двумя простыми тренировочными данными и относительно простым методом обновления мы, используя сглаживание поправки на основе скорости обучения, смогли очень быстро получить хорошую разделительную линию \( у=Ах \).
Теперь подав на вход данного классификатора некоторого жука \( (x,y) \), мы сможем определить, гусеница он или божья коровка, лишь взглянув на график. Стоит отметить, что классификатор будет тем лучше настроен, чем больше эталонных данных он обработает.
Реализация на Scilab настройки линейного классификатора по эталонной выборке
Для начала, создадим массив с жуками
// полная выборка
data = [3 1;
1 3;
2.5 2;
1.5 2.5;
2.9 1.5;
0.5 2;
0.83 2.45;
1.93 2.85;
2.91 1.15;
2.36 0.32];
Далее, чтобы не привязываться к размерностям и без опаски добавлять\удалять элементы выборки, узнаем число строк в матрице:
n = size(data, "r");
Пусть тренировочная выборка составляет 40% от всей выборки - на ней будем настраивать классификатор, на остальных 60% будем проверять классификатор:
dataTrainSize = round( 0.4 * n );
dataExpSize = n - dataTrainSize;
// выберем из исходной выборки с 1-го по dataTrainSize элемент
dataTrain = data(1:dataTrainSize, :);
// остальные элементы пойдут в матрицу для экспериментов
dataExp = data(dataTrainSize+1:n, :);
Зададим начальный коэффициент классификатора \( A \), скорость обучения \( L \), величину поправки \( d \):
k = .25;
L = .5;
d = .1;
Проведём в цикле обучение на тренировочной выборке:
for i = 1:dataTrainSize
// берём первую эталонную координату
x = dataTrain(i, 1);
//сичтаем для неё у
y = k * x;
//посмотрим, какой должен быть у эталонный
yEtalon = dataTrain(i, 2);
// эталонный у нужно подкорректировать -
// поднять, если это божья коровка
// и опустить, если это гусеница
if isLadyBug(x, yEtalon) then
yEtalon = yEtalon + d;
else
yEtalon = yEtalon - d;
end;
// считаем ошибку
e = yEtalon - y;
// счиатем корректирующий коэффициент
dk = L*e/x;
// корректируем классификатор
k = k + dk;
end
Функция проверки "божья ли коровка попалась" имеет вид:
function lb = isLadyBug(x, y)
lb = %T;
if (x < y) then
lb = %F;
end
endfunction
Чтобы посмотреть, как прошла тренировка классификатора, нарисуем жуков, покрасив божьих коровок красным, на которых тренировались и сам классификатор:
subplot(121);
xgrid;
xtitle('Тренировочная выборка', 'x', 'y');
for i = 1:dataTrainSize
plot(dataTrain(i, 1), dataTrain(i, 2), 'o');
if isLadyBug(dataTrain(i, 1), dataTrain(i, 2)) then
gce().children.mark_foreground = 5;
end
end
t = 0:3;
plot(t, k*t);
gca().data_bounds = [0,0; 3.2, 3.2];
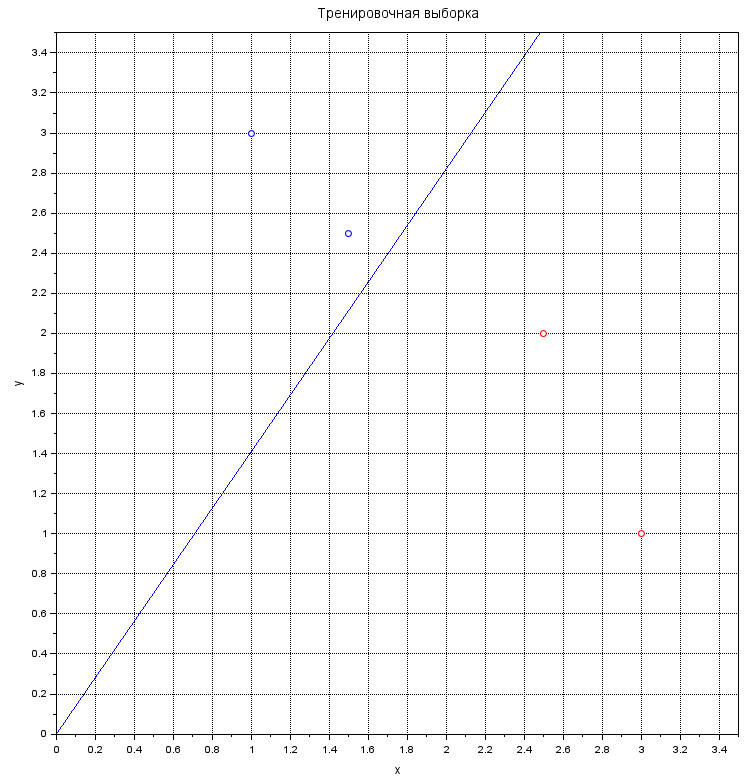
А теперь посмотрим, как классификатор разделяет оставшихся жуков:
subplot(122);
xgrid;
xtitle('Экспериментальная выборка', 'x', 'y');
plot(t, k*t)
gca().data_bounds = [0,0; 3.2, 3.2];
for i = 1:dataExpSize
plot(dataExp(i, 1), dataExp(i, 2), '*');
if isLadyBug(dataExp(i, 1), dataExp(i, 2)) then
gce().children.mark_foreground = 5;
end
end
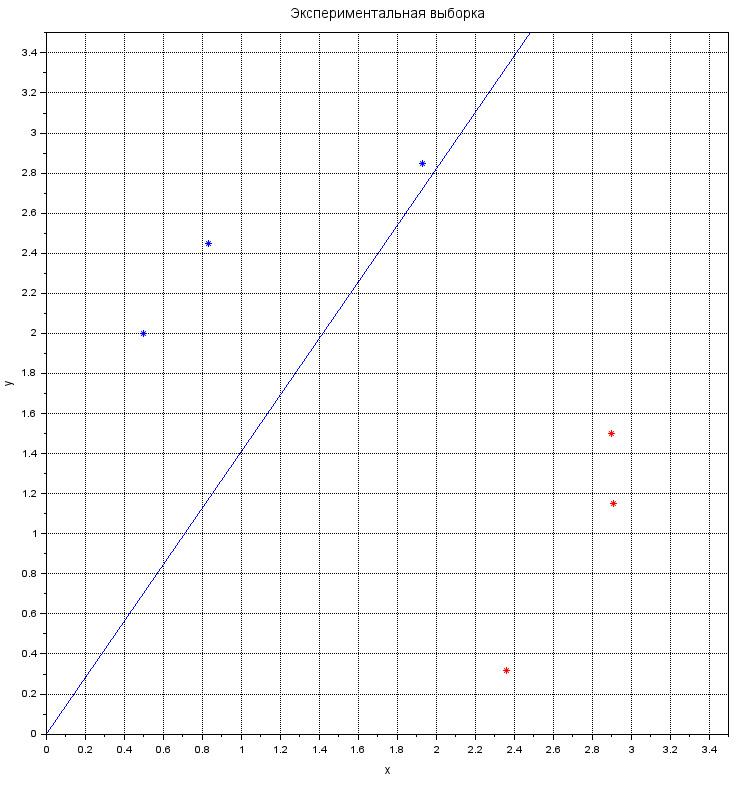
Прекрасно справляется. В конец выборки можно подобавлять значения и посмотреть, как справляется классификатор. А также, рекомендуется поизменять размер тренировочной выборки и параметры \( d \) и \( L \) .
Данная статья создана на основе чудесной книги(1) с реализацией автором приведённых примеров на Scilab.



Комментарии