Массивы в Scilab

Scilab - матрично-ориентированный язык. Под массивами в данном мат. пакете понимаются конструкции, используемые в линейной алгебре:  матрицы, векторы-строки и векторы-столбцы.

Под массивами в данном случае понимаются конструкции, используемые в линейной алгебре:  матрицы, векторы-строки и векторы-столбцы.

Важно! Нумерация элементов массива в Scilab начинается с 1.

2.1 Одномерные массивы (столбцы и строки)

Задать одномерный массив в Scilab можно следующим образом:

MAS = v1:d:vmax

Здесь MAS – имя переменной, куда будет записан сформированный массив, v1 – значение первого элемента массива, vmax – значение последнего элемента массива, d – шаг, с которым будет происходить формирование элементов.

Например, сформируем массив с элементами от 1 до 2 с шагом 0.1 (листинг 4).

M = 1:0.1:2;

\( M = \begin{pmatrix} 1. & 1.1 & 1.2 & 1.3 & 1.4 & 1.5 & 1.6 & 1.7 & 1.8 & 1.9 & 2. \end{pmatrix} \)

Сформировать одномерный массив можно и непосредственным перечислением всех его элементов через запятую или пробел:

MAS = [v1, v2, … , vmax] или MAS = [v1 v2 … vmax]

Отметим, что данные способы формируют вектор-строку в которую записаны всего vmax элементов.

Для поэлементного задания вектор-столбца нужно разделять элементы массива точкой с запятой «;», то есть, воспользоваться записью:

MAS = [v1; v2; …  ; vmax]

R = [1 0 1 2];
V = [1 0 1 2];

\( \begin{matrix} R = \begin{pmatrix} 1 & 0 & 1 & 2 \end{pmatrix} & V = \begin{pmatrix} 1 \\ 0 \\ 1 \\ 2 \end{pmatrix} \end{matrix} \)

Обращение к элементу массива происходит через указание номера элемента в круглых скобках у имени массива. Чтобы выбрать 2-й элемент одномерного массива MAS, необходимо ввести команду:

x =MAS(2);
disp(x); // выведет v2

Создадим вектор-строку row из 11 элементов, начиная с 0 с шагом 0.1. Это делается следующим образом:

row=0:0.1:1;

Сейчас row - это вектор-строка вида \( (0\; 0.1\; 0.2\; 0.3\; 0.4\; 0.5\; 0.6 \;0.7\; 0.8 \;0.9\; 1) \)

Получим 5-й эелемент вектор-строки row и выведем этот элемент:

x=row(5); // присвоили переменной х значение, записанное в 5-й столбец строки row
disp(x); // выведет 0.4

R = 0:0.1:1;
r2 = R(2);
r10 = R(10);  

\( \begin{matrix} R = \begin{pmatrix} 0. & 0.1 & 0.2 & 0.3 & 0.4 & 0.5 & 0.6 & 0.7 & 0.8 & 0.9 & 1. \end{pmatrix} & r2 = 0.1 & r10 = 0.9 \end{matrix} \)

2.2 Двумерные массивы (матрицы)

Двумерные массивы, или матрицы, также задаются при помощи квадратных скобок, при этом строки матрицы разделяются точкой с запятой «;», а столбцы -  запятой или пробелом (листинг 5).

Листинг 5. Задание матрицы поэлементно.

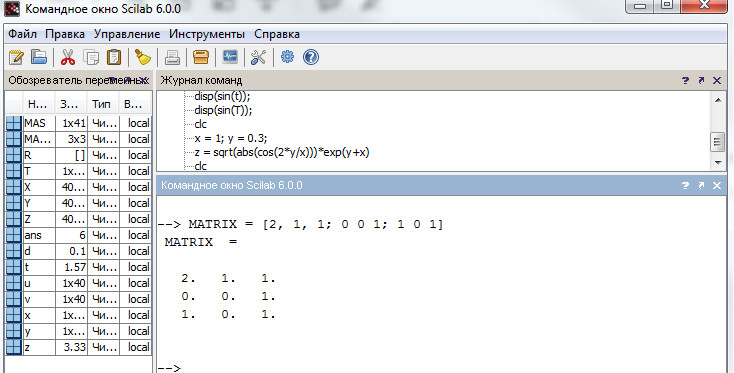
Кроме того, матрица может быть сформирована из векторов-строк или векторов-столбцов, заданных ранее (листинг 6).

Листинг 6. Задание матрицы из сформированных строк V1, V2, V3.

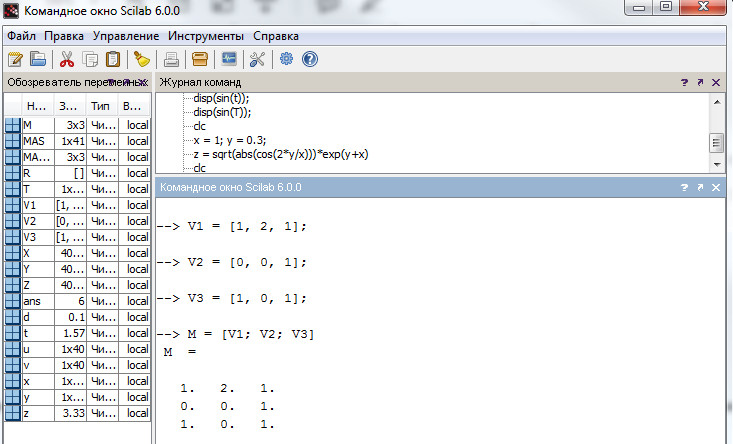
Обращение к элементу матрицы происходит через указание номера строки и столбца в круглых скобках у имени матрицы. Например, чтобы выбрать 3-й элемент из второй строки матрицы M, необходимо ввести команду:

M(2,3) // элемент из 2-й строки 3-го столбца 1

Отметим, что значения элементов матрицы можно использовать, присвоив их значения некоторым переменным, например:

x = M(2,3); или y = M(2,1)*M(1,1);

Важную роль в работе с матрицами играет знак двоеточия «:». Указывая его, можно получить целую строку или целый столбец. Например, чтобы выбрать третий столбец матрицы, нужно записать M(:,3). А чтобы получить все элементы второй строки, нужно записать M(2,:). Смотри (листинг 7).

Листинг 7. Выбор элементов m23, m12 матрицы М; 2-й строки и 3-го столбца матрицы М.

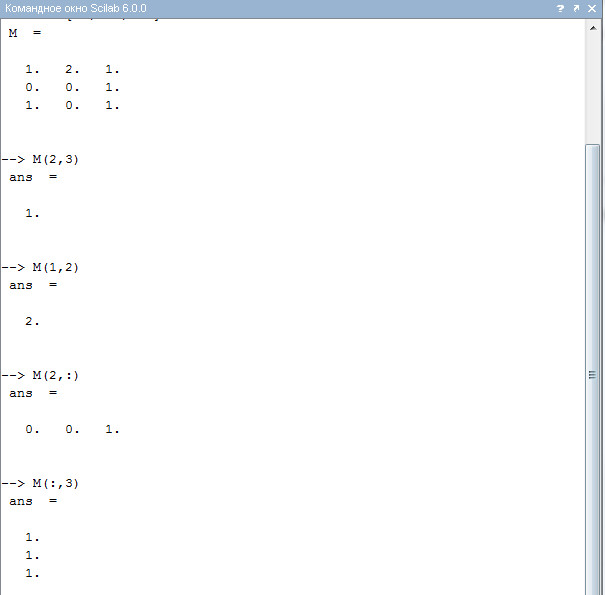
Отметим, что для работы с матрицами и векторами предусмотрены стандартные операции сложения «+», матричного умножения и умножения на число  «*», вычитания «-», возведения в степень «^», деления « / ».

Отдельно стоит выделить операции транспонирования «’» и поэлементного умножения « .* ».

Результаты операций с матрицами продемонстрированы ниже на Листинге 8.

Листинг 8. Операции матричного умножения, поэлементного умножения и транспонирования.

2.3 Специальные функции для векторов и матриц

В Scilab предусмотрены специальные функции для работы с матрицами. Эти функции обеспечивают быстрое создание распространенных типов матриц. Такими функциями являются следующие:

ones(m,n) – создание матрицы единиц из m строк и n столбцов;

zeros(m,n) – создание нулевой матрицы из m строк и n столбцов;

eye(m,n) - создание единичной матрицы из m строк и n столбцов.

Подробнее про них написано в статье Специальные матричные функции в Scilab

Кроме того, в мат. пакете есть ряд функций, полезных для решения задач линейной алгебры и устойчивости систем линейных дифференциальных уравнений.

det(M) – вычисление определителя квадратной матрицы;

inv(M) – вычисление матрицы, обратной к М, такой что M^-1M=E;

spec(M) – находит собственные числа матрицы М;

linsolve(M, b) – решает систему линейных уравнений Mx-b=0.

Подробнее про них написано в статье Функции для решения задач линейной алгебры в Scilab