Марковский процесс функционирования информационной системы с угрозами
Марковский случайный процесс с дискретным состоянием и дискретным временем
Предположим, что автоматизированная информационная системы может находиться в следующих n состояниях \( S_1, S_2, . . . , S_n\). При этом переход системы из i-го состояния в j-е характеризуется вероятностью \(p_{ij}\), где i, j = 1, 2, . . . , n.
Поскольку система может пребывать в одном из состояний, то для каждого момента времени t необходимо задать \(n^2\) вероятностей перехода \(p_{ij}\), которые удобно представить в виде следующей матрицы:
\begin{matrix} P= { \begin{pmatrix} p_{11} & p_{12} & ... & p_{1n} \\ p_{21} & p_{22} & ... & p_{2n} \\ ... & ... & ... & ... \\ p_{n1} & p_{n2} & ... & p_{nn} \end{pmatrix} (1)} \end{matrix}
Матрица (1) называется матрицей перехода системы.
В матрице перехода располагаются:
\(p_{ij} \) - вероятность перехода системы за один шаг из состояния \(S_i\) в состояние \(S_j\);
\(p_{ii}\) - вероятность задержки системы в состоянии \(S_i\).
Таким образом, в обозначении \(p_{ij} \) первый индекс указывает номер предшествующего состояния, а второй номер последующего.
Переходной вероятностью \(p_{ij} \) называют условную вероятность того, что из состояния \(S_i\), в котором система оказалась в результате некоторого испытания, безразлично какого номера, в итоге следующего испытания система перейдет в состояние \(S_j\).
Так как в каждой строке матрицы перехода помещены вероятности событий перехода из одного и того же состояния в любое возможное, то сумма вероятностей этих событий равна 1. Т.е. сумма значений в каждой строке матрицы должна быть равна 1:
\( \displaystyle\sum_{j=1}^{n} p_{ij} = 1, \quad i = \bar{1,n} \)
Марковский случайный процесс с дискретными состояниями и дискретным временем называют марковской цепью.
Для такого процесса моменты \( t_1, t_2, ...\), когда система может менять свое состояние, рассматривают как последовательные шаги процесса, а в качестве аргумента, от которого зависит процесс, выступает не время \( t\), а номер шага \( 1, 2, ... , k, ... \).
Случайный процесс в этом случае характеризуется последовательностью состояний \( S(0), S(1), S(2), ... , S(k), ... \), где
\(S(0)\) - начальное состояние системы (перед первым шагом);
\(S(1)\) - состояние системы после первого шага;
\(S(k)\) - состояние системы после k-го шага.
Вероятностями перехода системы за \( k \) шагов из \(S_i\) состояния в \(S_j\) называются вероятности \( P_{ij}(k) \) того, что в результате \( k \) шагов система перейдет из состояния \( S(0) = S_i \) в состояние \( S(k) = S_j \) \( i, j = 1, 2, ... \).
Например, \( P_{36}(8) \) - вероятность того, что за 8 шагов система перейдет из состояния \(S_3\) в \(S_6\).
Заметим, что при \(n = 1 \) вероятности состояний цепи Маркова \( P_{ij}(1) \) совпадают с переходными вероятностями \( p_{ij} \).
Кроме того, как и в случае (1) должно выполняться равенство:
\( \displaystyle\sum_{j=1}^{n} P_{ij}(k) = 1, \quad i = \bar{1,n}, \quad \forall k \quad\quad (2) \)
Начальным распределением вероятностей Марковской цепи называется распределение вероятностей состояний в начале процесса:
\( p_1(0), p_2(0), ... , p_n(0) \quad\quad (3) \).
Если для однородной Марковской цепи заданы начальное распределение вероятностей (3) и матрица P переходных вероятностей (1), то вероятности состояний системы \( p_i(k) (i = 1, 2, . . . ,) \) определяются по рекуррентной формуле:
\( p_{i}(k) = \displaystyle\sum_{j=1}^{n} p_{ji} \cdot p_{j}(k-1) = 1 \quad\quad (4) \)
Итак, у нас имеются:
Вектор \( (p_1(0), p_2(0), ... , p_n(0)) \) начального распределения (3). Это вероятности стартовать из каждого из состояний.
Переходные вероятности \( p_{ij} \). Это вероятности перейти из состояния \(S_i\) в \(S_j\) за 1 шаг. Из \( p_{ij} \) составлена матрица перехода (1).
Вероятности состояний системы \( p_{i}(k) \). Это вероятности оказаться в состояния \(S_i\) через \( k \) шагов.
Чудесная формула (4), по которой, зная начальное положение системы, можно рассчитать вероятность оказаться в том или ином состоянии через определённое число шагов.
Моделирование АИС с двумя зависимыми внутренними угрозами с помощью цепи Маркова
Пусть дана информационная система с двумя зависимыми внутренними угрозами, орграф которой изображен на рис. 1.
В качестве двух зависимых внутренних угроз могут быть следующие.
Неквалифицированная политика по управлению информационной безопасностью организации;
Отсутствие должной квалификации персонала по обеспечению деятельности и управлению информационной безопасностью.
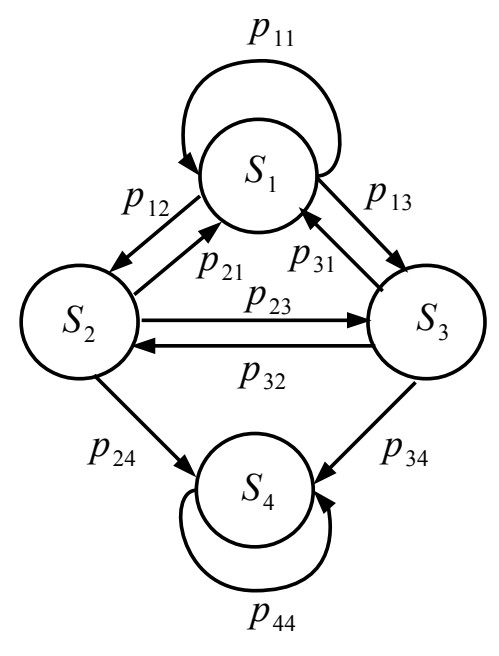
Данная система моделируется Марковской цепью. Она содержит невозвратные состояния, называемые поглощающими. Из поглощающего состояния нельзя перейти ни в какое другое. На графе поглощающему состоянию соответствует вершина, из которой не выходит ни одна дуга. Поглощающему состоянию соответствует вероятность, равная 1.
Пусть наша система может находиться в одном из четырех состояний:
\(S_1\) - состояние, в котором внутренние угрозы ИБ не проявились,
\(S_2\) - состояние, в котором первая внутренняя угроза ИБ проявилась с вероятность \(p_{12}\),
\(S_3\) - состояние, в котором вторая внутренняя угроза ИБ проявилась с вероятность \(p_{13}\),
\(S_4\) - поглощающее состояние, в котором внутренние угрозы ИБ реализовались с вероятностями \(p_{24}\) и \(p_{34}\) соответственно.
Для данной системы у нас заданы:
Вектор начального распределения:
\( (p_1(0), p_2(0), p_3(0) , p_4(0)) = (1, 0, 0, 0) \)
То есть, при запуске, мы стартуем всегда из 1-го состояния.
Матрица перехода:
\begin{matrix} P= { \begin{pmatrix} 0,2 & 0,3 & 0,5 & 0 \\ 0,4 & 0 & 0,3 & 0,3 \\ 0,1 & 0,4 & 0 & 0,5 \\ 0 & 0 & 0 & 1 \end{pmatrix} } \end{matrix}
А выяснить мы хотим вероятности состояний информационной системы через три шага, воспользовавшись формулой (4).
Приступим к реализации на scilab пошагового моделирования марковского процесса.
Зададим вектор начального распределения Po и матрицу вероятностей перехода P.
clc; clf;
Po = [1; 0; 0; 0];
P = [0.2 0.3 0.5 0; 0.4 0 0.3 0.3; 0.1 0.4 0 0.5; 0 0 0 1];
disp(P, "Матрица распределения вероятностей");
А далее итерационно воспользуемся формулой (4), бережно сохранив промежуточные результаты в Y.
// число шагов
n = 3;
// создадим пустой массив
Y = [];
// в первый столбец запишем имеющиеся значения начального распределения вероятностей Po
Y(:,1) = Po;
// двоеточие на первом месте означает, что будем брать все строки из первого столбца
for k = 2:n
// новый k-й столбец Y формируется как результат
// умножения транпонированной матрицы Р (см формулу 4 -> pji)
// на k-1 столбец матрицы У (т.е. вероятности состояния в k-1 момент времени)
Y(:,k) = P' * Y(:,k-1)
end
disp(Y, "Последовательность векторов оказаться в состояниях S1, S2 на 1,. . .," + string(n) + " шаге")
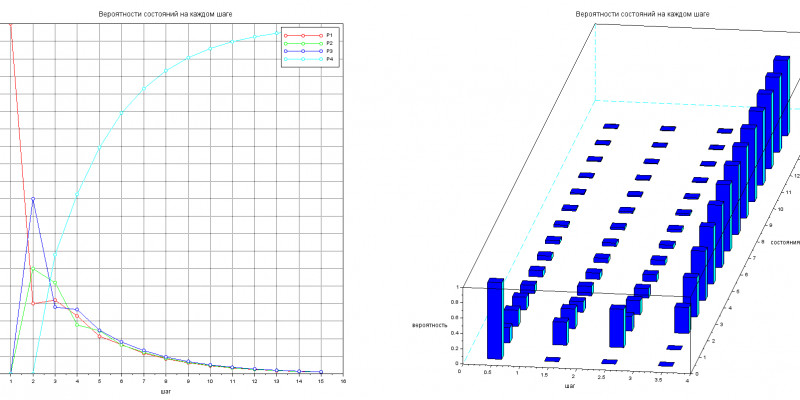
В консоли можно наблюдать за изменением вероятностей оказаться в каждом из 4-х состояний на 1,2 и 3-м шагах:

Если же число шагов увеличить до 10, то можно наблюдать, как система все вероятнее перейдёт в поглошающее 4-е состояние.

Отдельно стоит отметить, что сумма элементов вектора = 1.
Для пущей наглядности сходимости вероятностей, построим графики зависимости вероятностей Pj от числа шагов.
t = 1:n;
s = 1:3;
subplot(121);
plot(t, Y(1,:),'-ro', t,Y(2,:),'-go', t,Y(3,:),'-bo', t,Y(4,:),'-co'); xgrid;
xtitle("Вероятности состояний на каждом шаге", "шаг", "Вероятности");
legend("P1", "P2", "P3", "P4");
subplot(122);
bar3d(Y, alpha=75,theta=-25);
xtitle("Вероятности состояний на каждом шаге", "шаг", "состояния", "вероятность");
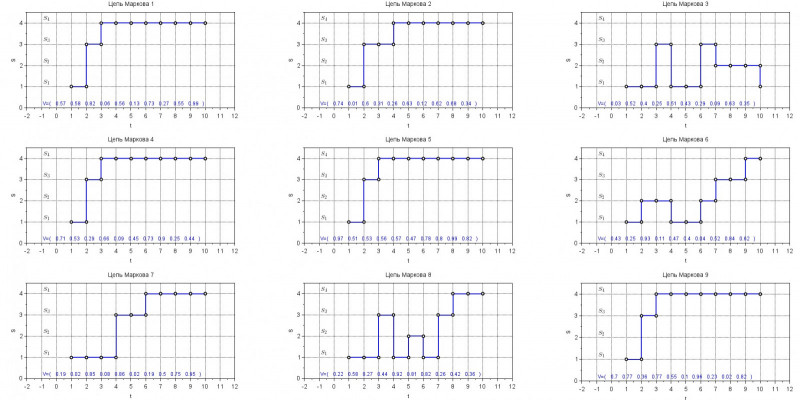
Серия экспериментов для цепи Маркова, граф которой изображён на рис.1
Посмотрим, действительно ли состояние 4 будет являться поглощающим в различных условиях. Для этого сгенерируем 9 случайных векторов состояний и, стартуя каждый раз из 1-го состояния, промоделируем поведение Марковской цепи с заданной матрицей перехода на протяжении 10-ти шагов.
clc; clf;
// Матрица перехода
probabilityMatrix = [0.2 0.3 0.5 0; 0.4 0 0.3 0.3; 0.1 0.4 0 0.5; 0 0 0 1];
probabilityMatrixDim = size(probabilityMatrix);
probabilityMatrixCols = probabilityMatrixDim(2);
// Состояния. Индекс строки S(j) - это эквивалент состояния Sj
statesVector = 1:probabilityMatrixDim(1);
markovChainSteps = 10;
// Моменты времени, в которые осуществляется переход из одного состояния в другое
t = 1:markovChainSteps;
// число строк в разбиении графического окна
winRows = 3;
// число столбцов в разбиении графического окна
winCols = 3;
//число экспериментов
winAxes = winRows*winCols;
Ниже моделирование цепи повторяется 9 раз.
for n = 1:winAxes
// генерируем случайный вектор состояний, которые выпали в n-e моменты
trainVector = ceil( 100 * rand(1, markovChainSteps, "uniform"))/100;
// Пусть стартовать будем всегда из 1-го состояния
Si = statesVector(1);
// Пока пустой массив, в который будем записывать вычисленные состояния
markovChain =[];
// Переменная для поиска состояния, в которое будем переходить
pmRowMax = 0;
for k = 1:markovChainSteps
// Запишем в цепь текущее состояние Si
chainMarkov(k) = Si;
// Номер строки матрицы перехода, в которой будем искать состояние, куда переходить
i = Si;
// Предположим, что состояние поглощающее
Sj = Si;
// Если выпала вероятность больше, чем текущая pii
if ( trainVector(k) > probabilityMatrix(i,i) ) then
// Пробежим всю i-ю строку матрицы
// т.е. будем менять столбцы j
// в поисках состояния, в которое можно перейти
pmRowMax = 0;
for j = 1:probabilityMatrixCols
// Если вероятность состояния
// оказалась больше элемента матрицы pij
// и данный элемент матрицы - самый большой из найденных
// и данный элемент матрицы позволяет перейти в другое состояние, т.е. не равен pii
if ( trainVector(k) > probabilityMatrix(i,j) ) &&
( probabilityMatrix(i,j) > pmRowMax ) &&
( probabilityMatrix(i,j) ~= probabilityMatrix(i,i) ) then
// обновляем максимальный элемент из найденных
pmRowMax = probabilityMatrix(i,j);
// считаем, что будем переходить в Sj состояние.
// т.к. pij говорит, что переходим из Si в Sj
// нам понадобится j - это столбца = номеру состояния, в которое переходим
Sj = j;
end
end
end
// после пробега всей строки
// обновляем текущее состояние
Si = Sj;
end
// рисование
subplot(winRows,winCols, n)
plot(t', chainMarkov);
ttl = "Цепь Маркова " + string(n);
xtitle(ttl, "t", "S");
xgrid;
// добавим надписи Si на координатную сетку и увеличим их шрифт до 3
// добавление $ ... $ внутри " ... " позволяет вводить текст в формате LaTex
// S_1 -это S с нижним индексом 1
for i = 1:probabilityMatrixCols
str = "$S_" + string(i) + "$";
xstring(-1, i, [str]); gce().font_size = 3;
end
str = string(trainVector);
xstring(-1, 0, ['V=(',str, ')']);
gce().font_size = 2;
gce().font_color = 2;
axe = gca();
axe.font_size = 3; //размер циферок на осях
axe.data_bounds=[-1, 0; markovChainSteps + 1, probabilityMatrixCols + .5]; // видимая область координатной сетки [Xmin, Ymin; Xmax, Ymsx]
mchain = axe.children.children(1); // выберем последний график на координатной сетке
mchain.polyline_style = 2; // соединение точек - лесенкой
mchain.foreground = 2; // цвет соединительных линий - синий
mchain.thickness = 2; // толщина соединительных линий
mchain.mark_mode = 'on'; // добавим кружочки в местах соединения линий
mchain.mark_style = 9; // тип кружка - не закрашенный
mchain.mark_size = 6; // размер кружка
end
В результате проведённых экспериментов, можно удостовериться, что попав в 4-е состояние, выбраться из него уже не удаётся.

Комментарии