Анимируем свёртку функций
Свёртка это математическая операция, применимая к \( f(t) \) и \( g(t) \), которая порождает третью функцию и определяется формулой:
\( y(t) = (f * g)(t) = \displaystyle\int_{-\infty}^{\infty}f(\tau)g(t-\tau)d\tau \) (1)
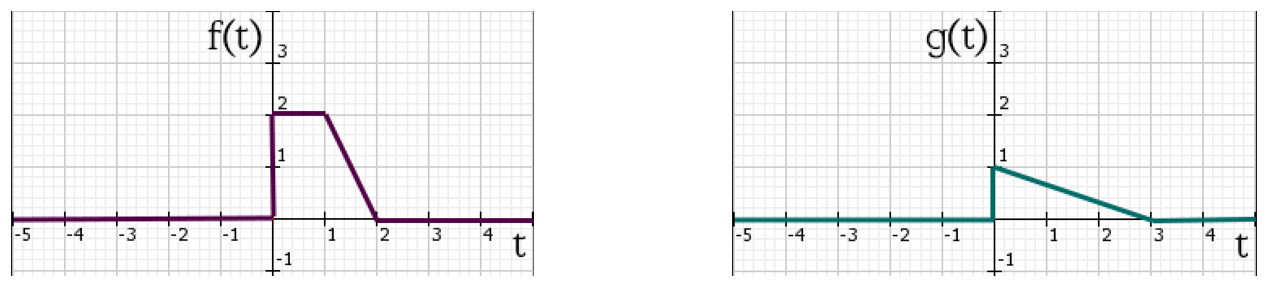
Рассмотрим реализацию свёртки двух сигналов на примере. Пусть сигналы \( f(t) \) и \( g(t) \) задаются в следующем виде:
\begin{matrix} f(t) = \begin{cases} 2, \quad 0 \leq t < 1 \\ -2t+4, \quad 1 \leq t < 2 \\ 0, \quad t<0 \text{ or } t \geq 2 \\ \end{cases} & g(t) = \begin{cases} 1, \quad t = 0 \\ 1 - \frac{1}{3}t, \quad 0 < t < 3 \\ 0, \quad t<0 \text{ or } t \geq 3 \\ \end{cases} \end{matrix}
Их графики, соответственно будут представлять собой ломаные, как показано ниже
Пример свёртки двух функций пошагово
Проведём пошаговую операцию свёртки двух сигналов, чтобы детально разобраться в смысле данной математической операции.
Итак, начнём с того, что в интегральном выражении у функции \( g(t-\tau) \) по переменной, которой производится интегрирование, стоит знак "-", а значит график нужно отразить по горизонтальной оси относительно оси ординат, как показано на рисунке ниже:
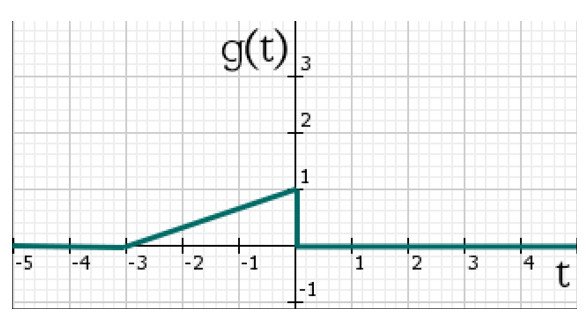
Выражение \( (t-\tau) \) означает, что движение будет происходить оси \( t \). Причём, если \( t<0 \), то график функции \( g(t) \) будет двигаться влево, при \( t \geq 0 \) движение будет происходить вправо.
Далее необходимо вычислить произведение \( g(t)(t-\tau) \) для каждого значения \( t \) и посчитать площадь получившейся в результате произведения двух графиков фигуры.
На рисунке ниже показано, какие случаи пересечений нам необходимо просчитать по мере движения графика по оси \( t \) .
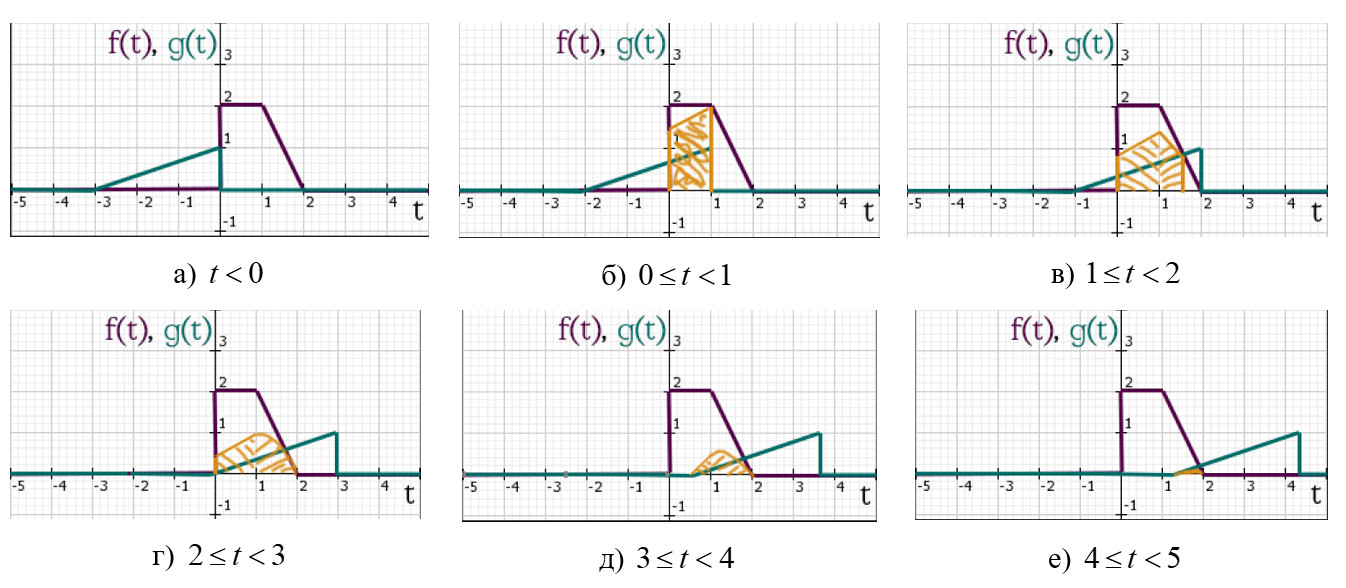
Остановимся на каждом из 6-ти случаев и произведём расчёты площадей получившихся фигур.
-
При \( t<0 \) графики сигналов не пересекаются, а значит и площадь фигуры их пересечения нулевая, то есть, результирующий интеграл примет вид:
\( \displaystyle\int_{-\infty}^{0}f(\tau)g(t-\tau)d\tau=0 \)
-
На интервале \( 0 \leq t < 1 \) сигнал \( f(t) \) представляет собой константу: \( f(t)=2 \) , а график сигнала \( g(t) \) - есть прямая \(1 - \frac{1}{3}t\). Исходя из вышесказанного, результатом сворачивания двух функций будет функция \( y(t) \) вида:
\( y(t) = \displaystyle\int_{0}^{t} 2 \left(1 - \frac{1}{3}(t-\tau)\right) d\tau = 2t - \frac{t^2}{3} \)
-
На интервале \( 1 \leq t < 2 \) результирующий интеграл можно разбить на 2 интеграла: первый вида, описанного в пункте b). Второй интеграл будет представлять собой площадь фигуры, имеющей стороны, описываемые прямыми \(1 - \frac{1}{3}t\) и \( -2t+4 \) . В результате, функция \( y(t) \) примет вид:
\( y(t) = \displaystyle\int_{0}^{1} 2 \left(1 - \frac{1}{3}(t-\tau)\right) d\tau + \displaystyle\int_{1}^{t} \left( 4 - 2\tau \right) \left(1 - \frac{1}{3}(t-\tau)\right) d\tau = \frac{t^3}{9} -\frac{5}{3}t^2 + \frac{13}{3}t - \frac{10}{9} \)
-
На интервале \( 2 \leq t < 3 \) результатом свёртки будет функция \( y(t) \):
\( y(t) = \displaystyle\int_{0}^{1} 2 \left(1 - \frac{1}{3}(t-\tau)\right) d\tau + \displaystyle\int_{1}^{2} \left( 4 - 2\tau \right) \left(1 - \frac{1}{3}(t-\tau)\right) d\tau = \frac{34}{9} -t \)
-
Предпоследним, дающим непустое пересечение графиков, будет интервал \( 3 \leq t < 4 \), который породит функцию \( y(t) \):
\( y(t) = \displaystyle\int_{t-3}^{1}2 \left(1 - \frac{1}{3}(t-\tau)\right) d\tau + \displaystyle\int_{1}^{2}\left( 4 - 2\tau \right) \left(1 - \frac{1}{3}(t-\tau)\right) d\tau = \frac{1}{3}t^2 -3t + \frac{61}{9} \)
-
Результирующей функцией на интервале \( 4 \leq t < 5 \) будет второе слагаемое из предыдущего случая со своими пределами интегрирования:
\( y(t) = \displaystyle\int_{t-3}^{2} \left( 4 - 2\tau \right) \left(1 - \frac{1}{3}(t-\tau)\right) d\tau = \frac{1}{9}t^3 + \frac{5}{3}t^2 - \frac{25}{3}t + \frac{125}{9} \)
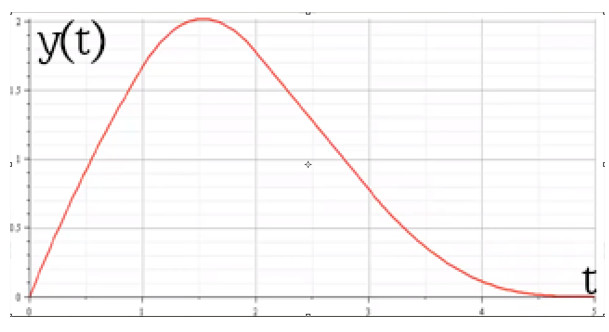
Таким образом, результатом свёртки игналов \( f(t) \) и \( g(t) \) будет функция \( y(t) \), задаваемая совокупностью уравнений:
\begin{matrix} y(t) = \begin{cases} 0, \quad t<0 \text{ or } t \geq 5 \\ 2t - \frac{t^2}{3}, \quad 0 \leq t < 1 \\ \frac{t^3}{9} -\frac{5}{3}t^2 + \frac{13}{3}t - \frac{10}{9}, \quad 1 \leq t < 2 \\ \frac{34}{9} -t, \quad 2 \leq t < 3 \\ \frac{1}{3}t^2 -3t + \frac{61}{9}, \quad 3 \leq t < 4 \\ \frac{1}{9}t^3 + \frac{5}{3}t^2 - \frac{25}{3}t + \frac{125}{9}, \quad 4 \leq t < 5 \\ \end{cases} \end{matrix}
На рисунке ниже приведена функция являющаяся результатом сворачивания двух сигналов на каждом из смысловых промежутков.
Реализация свёртки на Scilab
Для реализации в численных методах, рассматривается дискретный случай свертки двух функций \( f(j) \) и \( g(j) \)
\( z(k) = \displaystyle\sum_{j=max(1, k+1-L_g)}^{min(k,L_f)} f(j)\cdot g(k+1-j), \quad k=1,..,L_f+L_g \quad (3) \)
где \( L_f, L_g\) - количество элементов функций \( f(j) \) и \( g(j) \) соответственно.
Прежде всего, зададим функции \( f(j) \) и \( g(j) \) с помощью условных операторов в Scilab:
function ft = f(t)
ft = zeros(t);
for j = 1:length(t)
if ( t(j) >= 0 && t(j) < 1 ) then
ft(j) = 2;
elseif ( t(j) >= 1 && t(j) < 2 ) then
ft(j) = -2*t(j) + 4;
end;
end;
endfunction
function gt = g(t)
gt = zeros(t);
for j = 1:length(t)
if ( t(j) == 0 ) then
gt(j) = 1;
elseif ( t(j) >= 0 && t(j) < 3 ) then
gt(j) = -1/3*t(j) + 1;
end;
end;
endfunction
Далее на пишем функцию, реализующую свёртку, согласно формулы (3)
function cnv = myconv(f_, g_)
Lf = length(f_);
Lg = length(g_);
L = Lf + Lg - 1;
cnv = zeros(1,L);
for k = 1:L
jmin = max(1, k + 1 - Lg);
jmax = min(k, Lf);
for j = jmin:jmax
cnv(k) = cnv(k) + f_(j) * g_(k + 1 - j);
end
end
endfunction
И посмотрим, сойдётся ли результат, полученный с помощью нашей функции \( myconv() \) с результатом, полученным при использовании встроенной функции \( conv() \)
d = 1e-1;
Tmin = -1; Tmax = 4;
t = Tmin:d:Tmax;
plot( conv(f(t), g(t)), 'r' );
plot( myconv(f(t), g(t)), 'b--' );
xgrid();xtitle("Свёртка двух сигналов","t", "y(t)");
legend("Встроенная свёртка", "Своя свёртка");
gca().children.children.thickness = 2;
Глядя на изображение ниже, можно с уверенностью сказать, что результаты совпадают :)
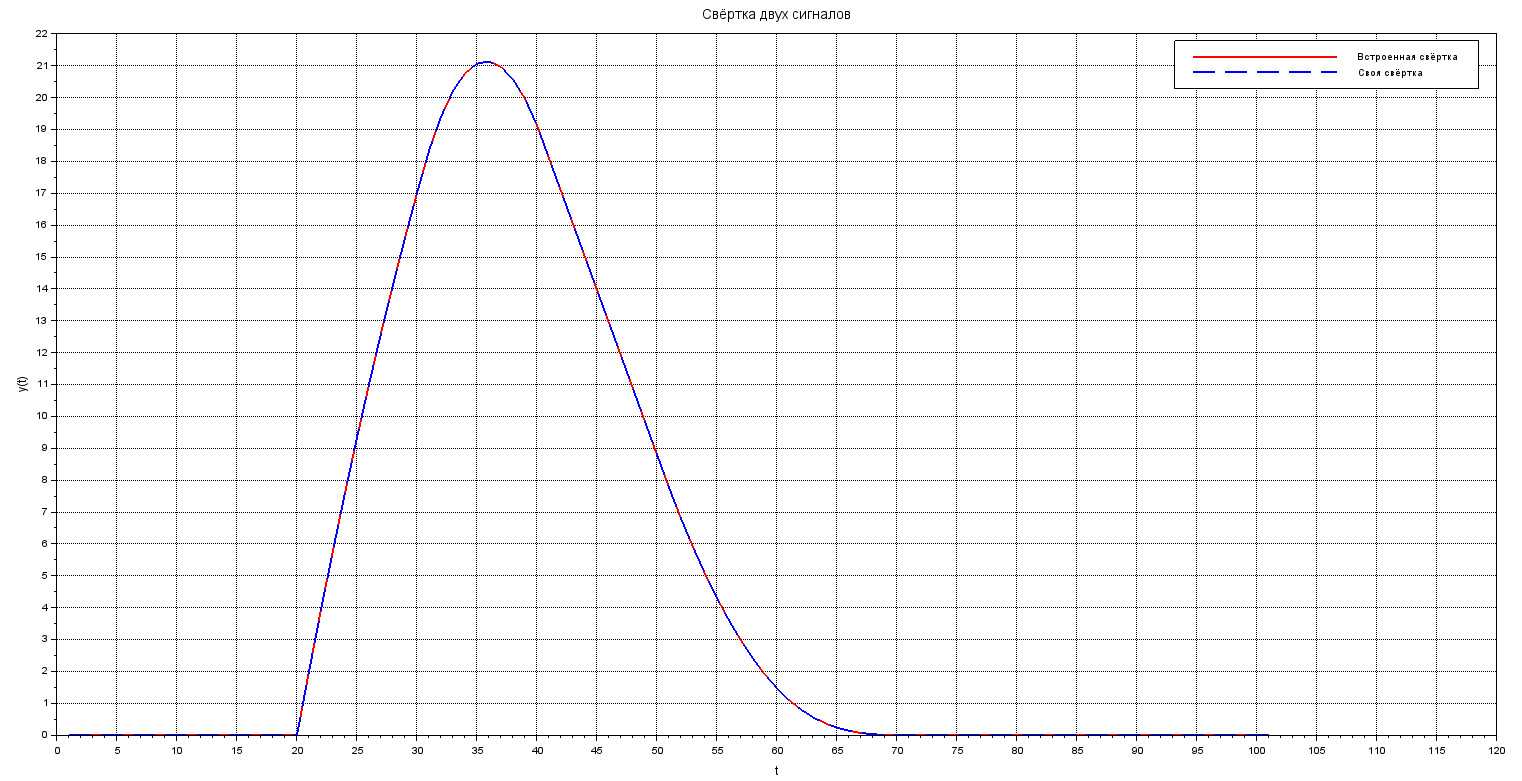
Вот только масштаб и отсчёты не похожи на наши задынные промежутки. Поэтому, проведём масштабирование результатов.
Корректировка результатов свёртки
Для корректного отображения результирующего графика нам потребуется несколько модифицировать функцию \( myconv() \). Прежде всего, заведём переменную, отвечающую за сдвиг результата по горизонтальной оси:
N = (2*abs(Tmin))/d;
И изменим функцию \( myconv() \) следующим образом:
function cnv = myconv(f_, g_, shift)
Lf = length(f_);
Lg = length(g_);
L = Lf + Lg - 1;
cnv = zeros(2,L);
for k = 1:L
jmin = max(1, k + 1 - Lg);
jmax = min(k, Lf);
cnv(1,k) = k - shift;
for j = jmin:jmax
cnv(2,k) = cnv(2,k) + f_(j) * g_(k+1-j);
end
end
endfunction
Посмотрим, как теперь будет выглядеть результат:
myconv_scalled = d * myconv(f(t), g(t), N);
plot(myconv_scalled(1,:), myconv_scalled(2,:), 'b--' );
xgrid();xtitle("Свёртка двух сигналов","t", "y(t)");
legend("Своя свёртка");
gca().children.children.thickness = 2;
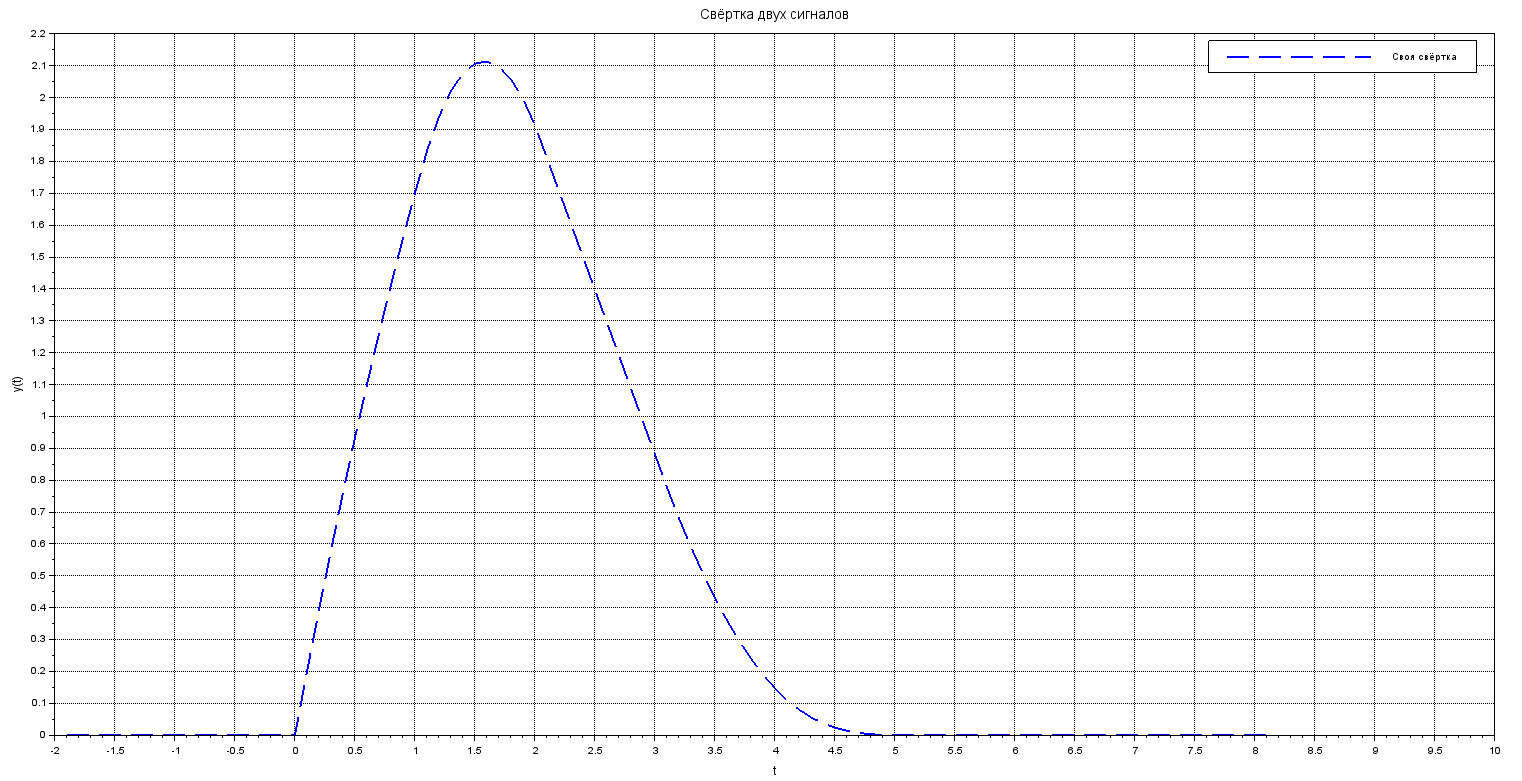
Стало значительно лучше: мы укладываемся в интервал и стартуем из нуля.
Реализация анимации свёртки двух сигналов
Прежде всего, выведем графики сигналов, которые сворачиваем:
shift = 2*abs(Tmin);
plot(t, f(t), "r" );
plot(-t - shift, g(t), "g" );
xgrid();xtitle("Свёртка двух сигналов","t", "f(t), g(t), y(t)");
legend("f(t)", "g(-t)");
conv_axes = gca();
conv_axes.data_bounds=[-5 -0.1; 8 max(myconv_scalled(2,:))];
conv_axes.children.children.thickness = 2;
Чтобы графики выглядели поприличнее, нужно уменьшить шаг дискретизации, например до \( d=0,01 \) и настроить их толщину с помощью \( gca().children.children.thickness \)
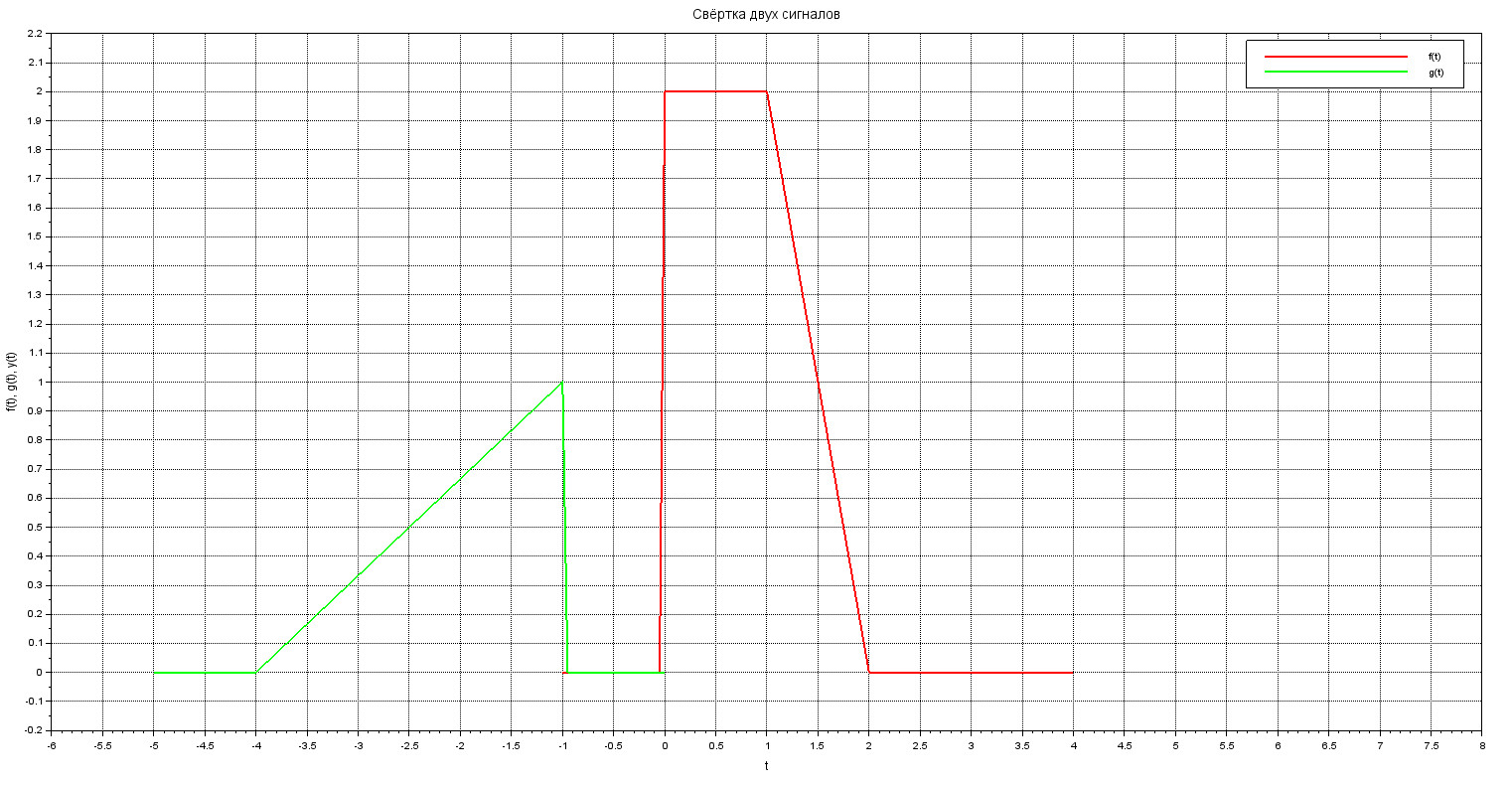
Осталось лишь реализовать анимационный цикл.
В статьедано описание основ анимации в Scilab.
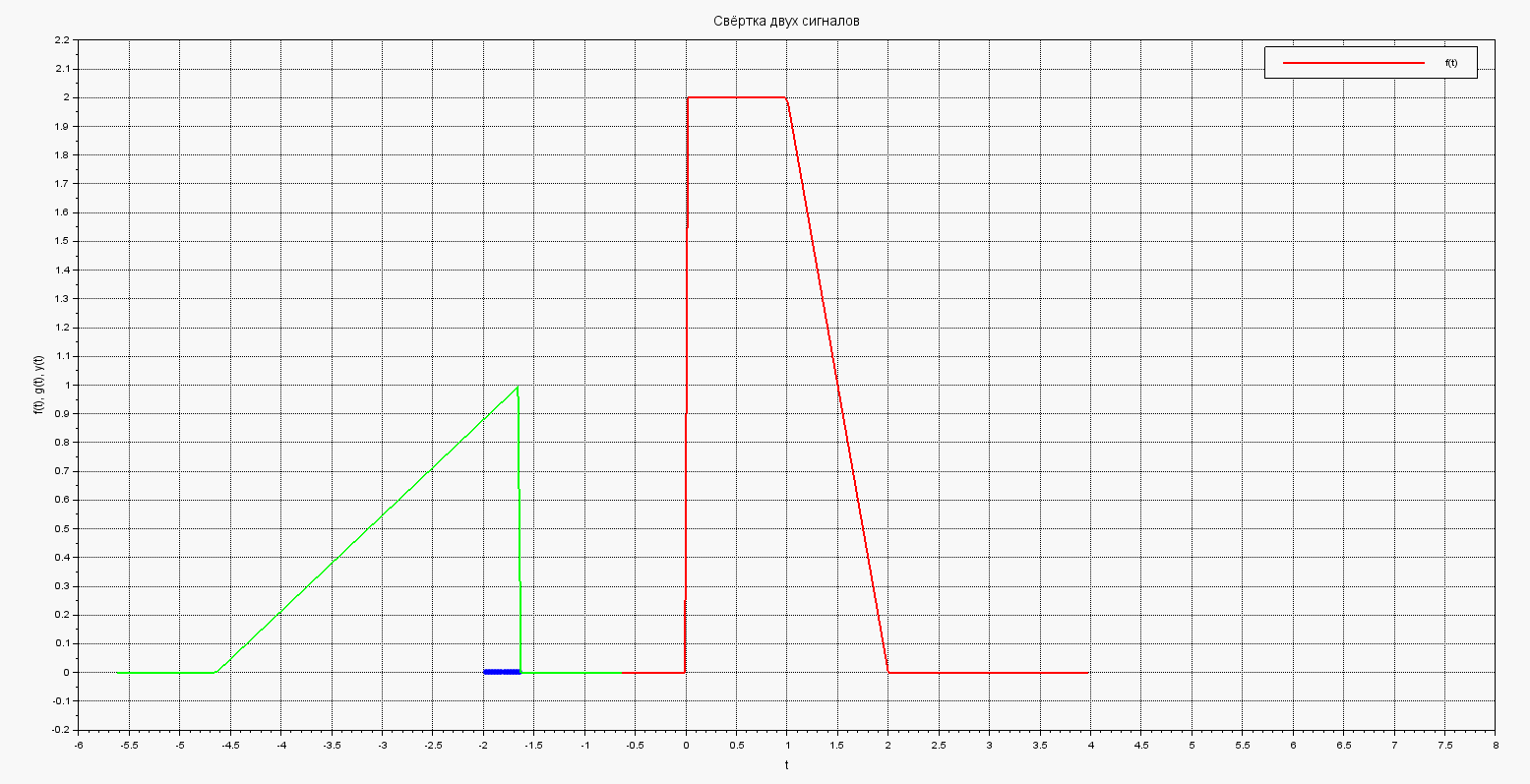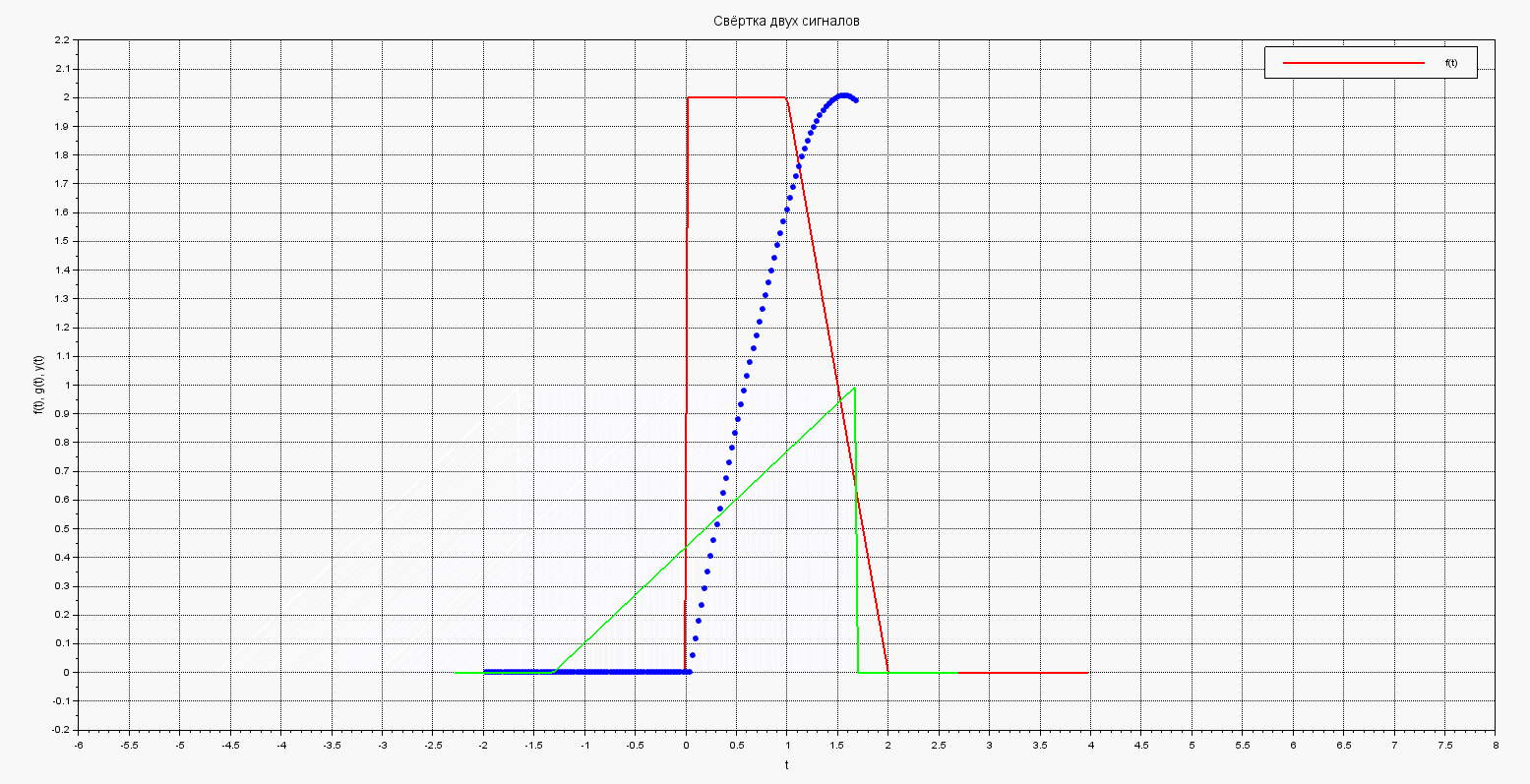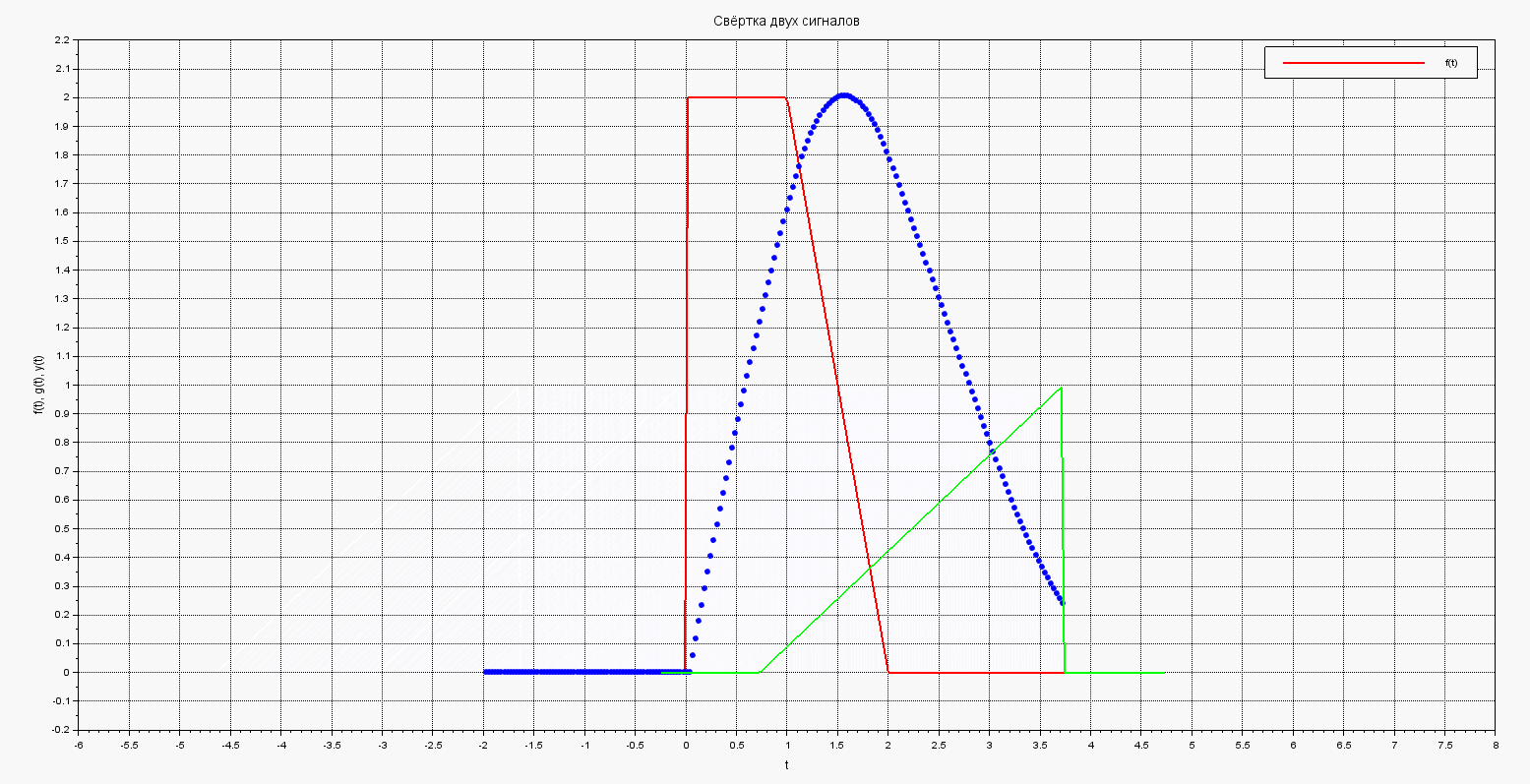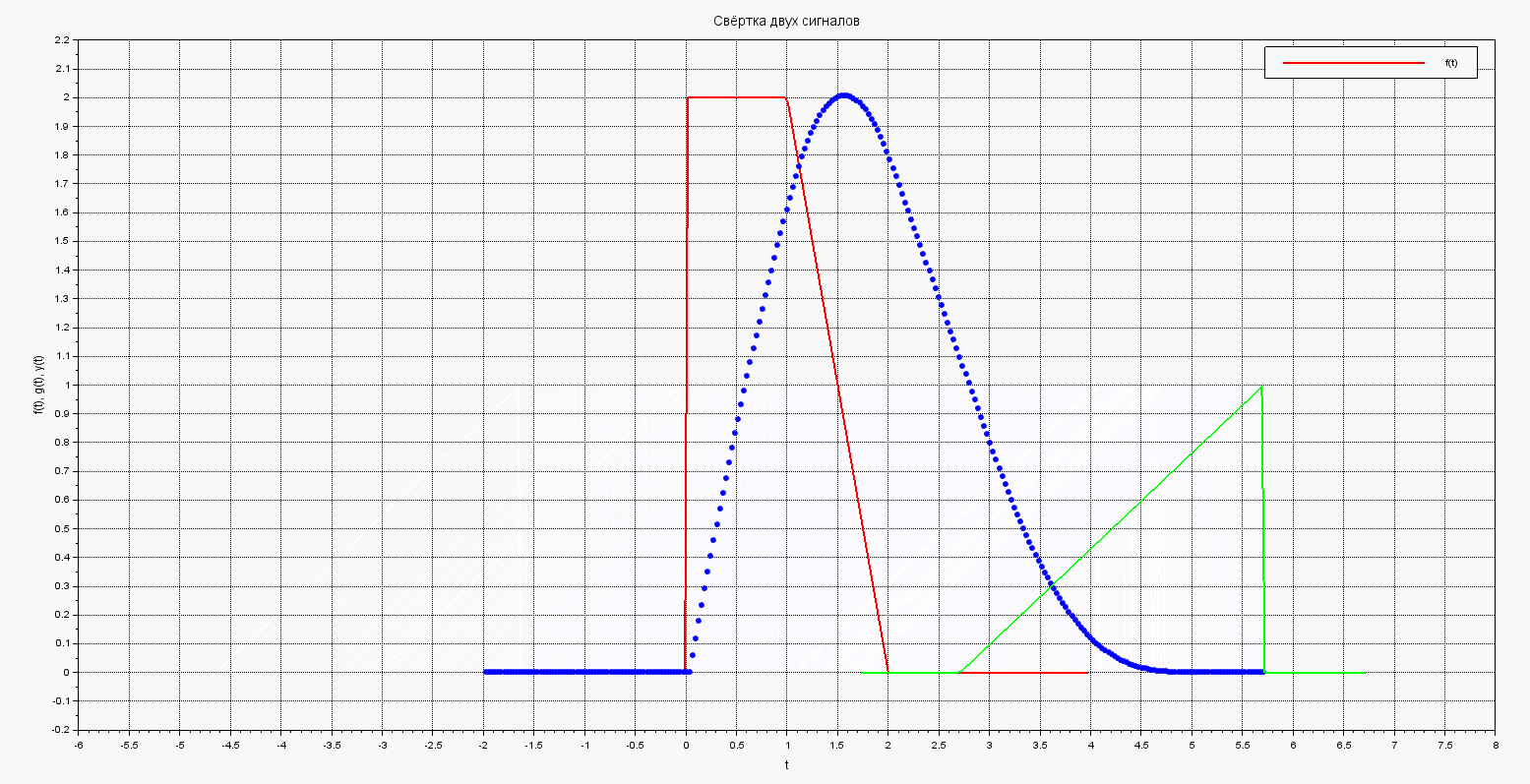
Здесь на каждом шагу цикла мы рисуем i-ю точку свёртки, а зелёный график рисуем и стираем, что имитирует его движение.
i = 1; t_ = Tmin; g_inv = g(t);
while ( (i <= length(myconv_scalled(2,:))) && (t_ < 2*Tmax) )
drawlater();
sca(conv_axes);
plot(myconv_scalled(1,i), myconv_scalled(2,i), '.-b');
plot(-t - shift + i*d, g_inv, 'g');
conv_axes.children.children.thickness = 2;
realtime(i);
delete(conv_axes.children.children(3));
drawnow();
i = i+1;
t_ = i*d;
end
В результате получим такую анимированную картинку движения графика и построения результирующего интеграла-свёртки:

Комментарии