Построение графиков Scilab

Математический пакет Scilab располагает широким и гибко настраиваемым аппаратом для построения двумерных графиков и трёхмерных изображений.

Данная статья получила продолжение: Как настраивать толщину и начертание графиков в Scilab и дополнительный разбор Настройки графиков: свойства осей и сетки.

Перечислим основные функции для оформления графика:

xgrid() - добавление сетки на график;
xtitle("Название графика", "Название оси абсцисс", "Название оси ординат") - добавление подписей;
legend(.., , .. ) - создание легенды с перечнем всех отображенных графиков в системе координат;
subplot(mnk) - функция разделения окна на матрицу, содержащую строк, $с т о л б ц о в$ , а - это номер ячейки, в которой будет отображен график.

Например, subplot(312) разобъёт графичекое окно на 3 строки, 1 столбец и нарисует график во второй ячейке:

Расположение графика в графическом окне subplot(312).

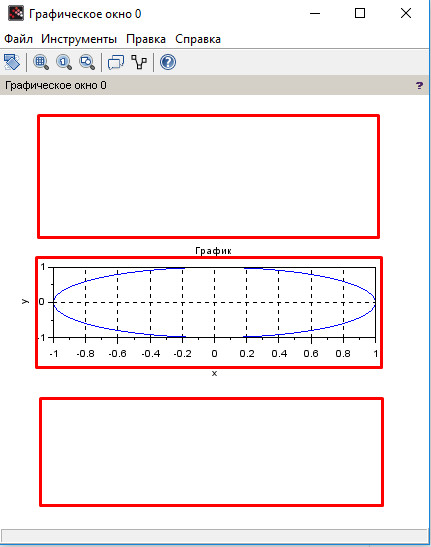
Например, subplot(234) разобъёт графичекое окно на 2 строки, 3 столбца и нарисует график в четвёртой ячейке:

Расположение графика в графическом окне subplot(234).

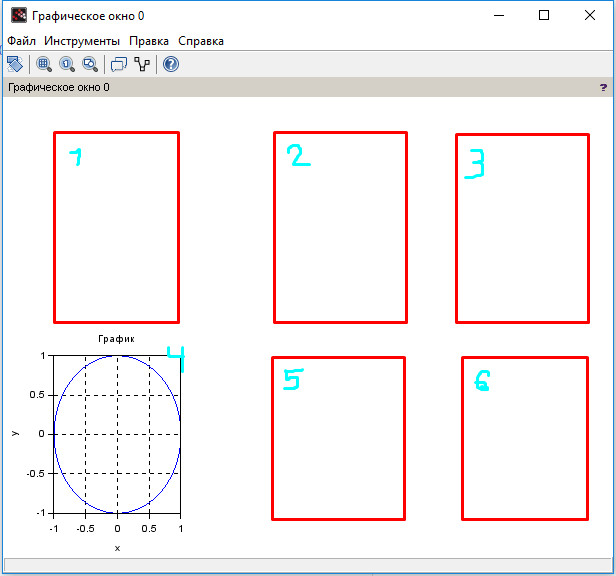
5.1 Двумерные графики

Для построения графиков, в которых положение точки задаётся двумя величинами, в Scilab нужно воспользоваться функцией plot(x, y , s). Здесь первая переменная $х$ - массив абсцисс, $у$ - массив ординат, - необязательный параметр, отвечающий за цвет графика, толщину и начертание линии.

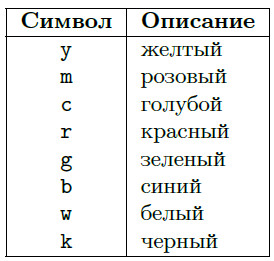
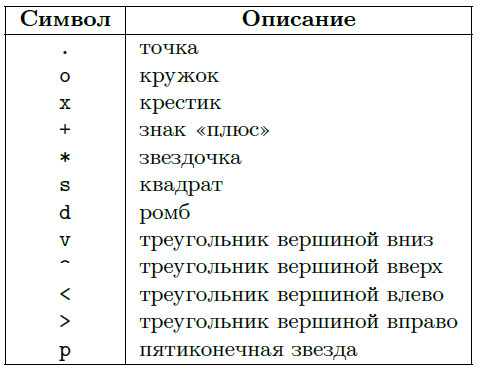
Установить желаемый вид и цвет графика можно, указав строковый параметр , который может состоять из одного, двух или трёх символов, определяющие соответственно: цвет линии, тип маркера, тип линии графика. Возможные значения перечислены в таблицах 2-4.

Таблица 2. Символы, определяющие цвет линии графика.

Таблица 3. Символы, определяющие тип линии графика.

Таблица 4. Символы, определяющие тип маркера

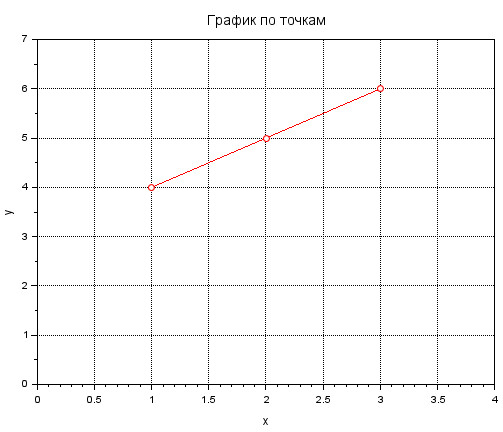
Построение графика по точкам

Для построения графика по точкам необходимо задать два массива: абсцисс и ординат, после чего воспользоваться функцией . Для демонстрации используем пример, любезно предоставленнный miklev:

x=[1, 2, 3]; // задаём массив точек по горизонтали
y=[4, 5 ,6]; // задаём массив точек по вертикали
  
plot(x, y, 'r-o'); // строим график по данным. Соединительные элементы -  крожочки
xtitle('График по точкам', 'x', 'y');
xgrid();

gca().data_bounds = [0, 4, 0, 7]; // изменяем видимую область

Программа построения графиков по точкам в scilab

Построение графиков в scilab

Построение графика по заданному уравнению

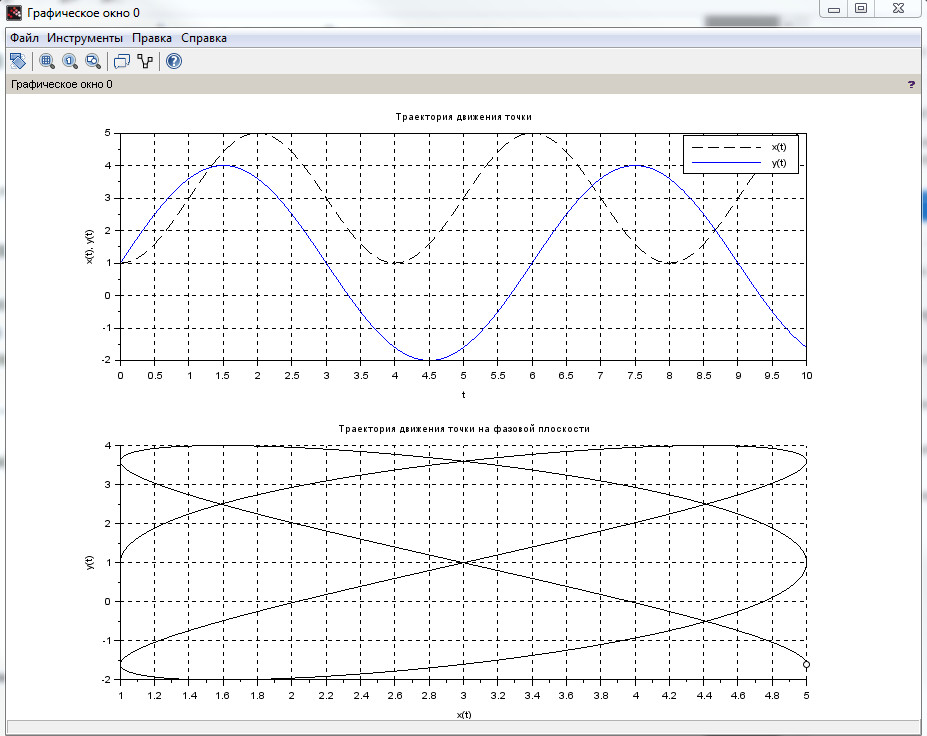
Для демонстрации работы функции plot() построим графики траектории движения точки по заданным уравнениям на плоскости и в заданном диапазоне времени T (таблица 5). Определим внешний вид каждого из графиков, а также оформим систему координат со всеми необходимыми подписями (листинг 13). Результат работы программы представлен на рис. 7.

Таблица 5. Уравнения движения материальной точки и промежуток времени.

Рисунок 7. Построение графиков движения материальной точки.

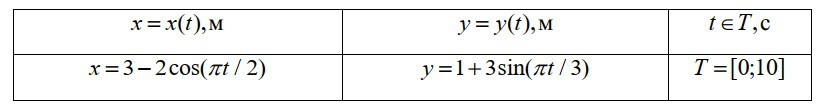
/* графики траектории движения материальной точки */

// очищаем область консоли и графического окна
clc; clf; 

// создаём пользовательскую функцию для координаты х
function z = X(t)
    z = 3 - 2*cos(%pi*t/2);
endfunction;

// создаём пользовательскую функцию для координаты y
function z = Y(t)
    z = 1 + 3*sin(%pi*t/3);
endfunction;


d = 1e-2;    // задаём шаг
T = 0:d:10;   // задаём диапазон времени

x = X(T);   // вызываем пользовательскую функцию X
y = Y(T);   // вызываем пользовательскую функцию Y

subplot(211);       // разделяем графическое окно на 2 строки 
plot(T, x, "k--");  // строим график x(t)
plot(T, y);         // строим график у(t) в той же системе координат
xgrid; 
xtitle("Траектория движения точки", "t", "x(t), y(t)"); 
legend("x(t)", "y(t)");

subplot(212);  
xgrid; 
xtitle("Траектория движения точки на фазовой плоскости", "x(t)", "y(t)"); 
comet(x, y);      // строим анимированную траекторию движения точки на фазовой плоскости

Листинг 13. Программа построения графиков движения материальной точки.

5.2 Построение трёхмерных изображений

Для построения поверхности в Scilab используются функции plot3d( plot3d1) и plot3d2(plot3d3). Их отличие состоит в том, что первая пара функций plot3d( plot3d1) строит поверхность из отдельно стоящих друг от друга грани (залитую одним цветом и залитую различными цветами соответсвенно), а вторая пара plot3d2(plot3d3) - цельное геометрическое тело.

Процесс построения графика функции вида можно разделить на 3 этапа:

Создание прямоугольной сетки с помощью функции linspace();
Вычисление значений функции в узлах сетки;
Вызов функции plot3d() или plot3d2().

В качестве примера, построим сферу в трехмерной системе координат с помощью функций plot3d1 и plot3d2.

Рисунок 8. Сфера, заданная параметрически, построенная с помощью функции plot3d1 (слева) и plot3d2 (справа).

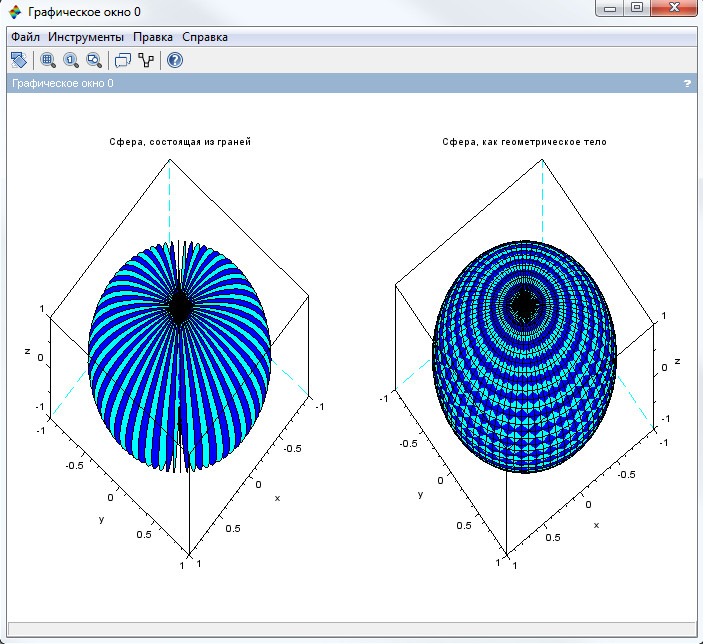
Поверхность сферы в декартовых координатах параметрически задаётся системой уравнений: ,
независимые переменные $и$ изменяются на промежутке . Результат работы программы представлен на рис.8, исходный код на листинге 14.

/* работа с трёхмерными графиками */

u = linspace(-%pi, %pi, 40); // задаём сетку для параметра u с 40 значениями в указанном диапазоне
v = linspace(-%pi, %pi, 40); // задаём сетку для параметра v с 40 значениями в указанном диапазоне
/* массивы u и v должны иметь одиноковый размер! */

/* Формируем матрицы значения для каждой координаты */
X = cos(u)'*cos(v);
Y = cos(u)'*sin(v);
Z = sin(u)'*ones(v);

/* Строим трёхмерные графики */
subplot(121);
plot3d(X,Y,Z);
xtitle("Сфера, состоящая из граней", "x", "y", "z");

subplot(122);
plot3d2(X,Y,Z);
xtitle("Сфера, как геометрическое тело", "x", "y", "z");

Листинг 14. Программа, реализующая построения трехмерного изображения сферы с помощью функции plot3d1 и plot3d2.

Обратите внимание, что при построении графиков поверхностей заданных параметрически, $и$ , необходимо сформировать матрицы $и$ одинакового размера. Для этого массивы $и$ должны иметь одинаковый размер.

Кроме того, если какая-либо функция из $и л и$ зависит только от одного параметра $и л и$ , необходимо провести векторное умножение на единичный вектор ones() размерности, равной размерности параметра, от которого эта функция не зависит (см. строку 10 листинга 14).