Пример создания GUI-приложения в Scilab
GUI ( Graphic User Interface ) это пользовательский интерфейс, позволяющий взаимодействовать с приложением, написанным на языке Scilab, человеку, не имеющему специальных знаний в программировании. Графический интерфейс пользователя определяет взаимодействие с пользователем на уровне визуализированной информации: заполнение форм, выбор пунктов меню, нажатие кнопок, заполнение полей ввода.
Мы рассмотрим создание графического приложения, реализующего возможность ввода пользователем параметров системы и построения графика в визуальном окне. Для этого будем решать следующую задачу.
Груз массы \( m \) кг. находится на пружине жёсткости \( c \) H/м и движется в жидкости. Сила сопротивления движению груза пропорциональна первой степени скорости груза \( R = -\alpha v, \alpha>0 \). Определить движение груза, если в начальный момент груз был смещён из положения равновесия на \( x_0 \) метров и отпущен без начальной скорости.
По 2-му закону Ньютона, движение груза описывается с помощью дифференциального уравнения 2-й степени, которое имеет вид:
\( \ddot{mx} = -cx - \alpha \dot{x} \)
и начальными условиями \( x(0) = x_0, \dot{x}(0)=0 \).
Как известно, ДУ второго порядка сводится к системе в нормальной форме Коши, состоящей из двух уравнений первой степени. Введём новые переменные \( z_1, z_2 \) и сделаем необходимые переобозначения в исходной системе:
\begin{cases} z_1 = x \\ z_2 = \dot{x} \end{cases} \begin{cases} \dot{z}_1 = z_2 \\ \dot{z}_2 = -{1 \over m}(cz_1 + \alpha z_2) \end{cases}
Прежде всего создадим графическое окно, на котором будут располагаться поля ввода параметров системы и график движения груза (рис. 15 и листинг 20).
xdel();clc;
mainWindow = createWindow();
mainWindow.figure_name = "Решение задачи о подвешенном на пружине грузе";
На следующем этапе разместим в этом окне 6 полей для ввода параметров системы с соответствующими названиями (см. Рисунок 16).
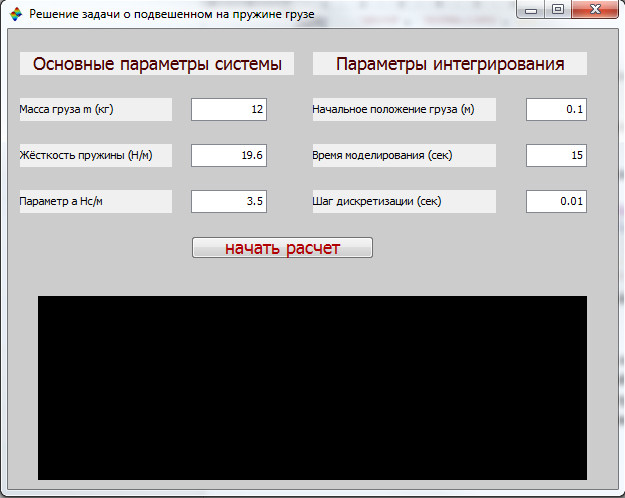
Обратите внимание, что положение каждого из элементов задается в относительных единицах «Units», причем начало отсчета находится в левом нижнем углу графического окна (листинг 21).
sparamTitle = uicontrol(mainWindow, ...
"style","text",...
"string","Основные параметры системы",...
"fontSize", 18, ...
"horizontalAlignment","center",...
"ForegroundColor", [0.3,0,0], ...
"units", "normalized", ...
"position", [0.02 0.9 0.45 0.05]);
//масса груза
mLabel = uicontrol(mainWindow, ...
"style","text",...
"string","Масса груза m (кг)",...
"units", "normalized", ...
"position", [0.02 0.8 0.25 0.05]);
mEdit=uicontrol(mainWindow, ...
"style", "edit",...
"string", "12",...
"horizontalAlignment","right",...
"units", "normalized", ...
"position", [0.3 0.8 0.125 0.05]);
//Жёсткость пружины
cLabel = uicontrol(mainWindow, ...
"Style","text",...
"String","Жёсткость пружины (H/м)",...
"units", "normalized", ...
"position", [0.02 0.7 0.25 0.05]);
cEdit=uicontrol(mainWindow, ...
"Style", "edit",...
"String", "19.6",...
"HorizontalAlignment","right",...
"units", "normalized", ...
"position", [0.3 0.7 0.125 0.05]);
//параметр альфа
aLabel = uicontrol(mainWindow, ...
"Style","text",...
"String","Параметр а Нс/м ",...
"units", "normalized", ...
"position", [0.02 0.6 0.25 0.05]);
aEdit=uicontrol(mainWindow, ...
"Style", "edit",...
"String", "3.5",...
"HorizontalAlignment","right",...
"units", "normalized", ...
"position", [0.3 0.6 0.125 0.05]);
Добавим параметры для численного решения задачи: это начальное положение груза, время моделирования и шаг дискретизации.
sparamTitle = uicontrol(mainWindow, ...
"style","text",...
"string","Параметры интегрирования",...
"fontSize", 18, ...
"horizontalAlignment","center",...
"ForegroundColor", [0.3,0,0], ...
"units", "normalized", ...
"position", [0.5 0.9 0.45 0.05]);
//Начальное положение груза
x0Label = uicontrol(mainWindow, ...
"Style","text",...
"String","Начальное положение груза (м)",...
"units", "normalized", ...
"position", [0.5 0.8 0.3 0.05]);
x0Edit=uicontrol(mainWindow, ...
"Style", "edit",...
"String", "0.1",...
"HorizontalAlignment","right",...
"units", "normalized", ...
"position", [0.85 0.8 0.1 0.05]);
//Время моделирования Tmax=
tmaxLabel = uicontrol(mainWindow, ...
"Style","text",...
"String","Время моделирования (сек)",...
"units", "normalized", ...
"position", [0.5 0.7 0.3 0.05]);
tmaxEdit=uicontrol(mainWindow, ...
"Style", "edit",...
"String", "15",...
"HorizontalAlignment","right",...
"units", "normalized", ...
"position", [0.85 0.7 0.1 0.05]);
//Шаг дискретизации
dLabel = uicontrol(mainWindow, ...
"Style","text",...
"String","Шаг дискретизации (сек)",...
"units", "normalized", ...
"position", [0.5 0.6 0.3 0.05]);
Рассмотрим подробно добавление UI - элемента на примере создания текстового поля для ввода пользователем массы груза.
//масса груза
mLabel = uicontrol(mainWindow, ...
"style","text",...
"string","Масса груза m (кг)",...
"units", "normalized", ...
"position", [0.02 0.8 0.25 0.05]);
mEdit=uicontrol(mainWindow, ...
"style", "edit",...
"string", "12",...
"horizontalAlignment","right",...
"units", "normalized", ...
"position", [0.3 0.8 0.125 0.05]);
Элементы пользовательского интерфейса создаются с помощью функции uicontrol() с различными параметрами. Первый параметр обозначает окно, на которое будет добавлен элемент, в нашем случае это параметр mainWindow.
Далее указывается тип (style) создаваемого элемента, у нас это text для лейбла поля и edit для самого поля ввода массы \(m \).
Следующим параметром, как правило, идет значение создаваемого элемента по умолчанию (string), мы задали название лейбла Масса груза m и значение в 12 кг. для поля edit.
Параметры units и position задают положение элемента на графическом окне mainWindow. Значение normalized данного параметра означает, что элемент будет спозиционирован относительно на графическом окне. Значение [0.3 0.8 0.125 0.05] означает, что элемент будет помещен в точку (0.3; 0.8) графического окна и займёт 0.125 относительных единиц в ширину и 0.05 относительных единиц в высоту.
Нам осталось добавить кнопку, по которой будут происходить вычисления и зарезервировать место для вывода графика движения груза.
Создадим кнопку «начать расчет», по нажатию на которую, будет вызываться функция startCalculus() (см. Листинг 22 и рисунок 17).
//кнопка начать расчет
startButton = uicontrol(mainWindow, ...
"Style","pushbutton",...
"String","начать расчет",...
"fontSize", 18, ...
"ForegroundColor", [0.7,0,0], ...
"units", "normalized", ...
"position", [0.3 0.5 0.3 0.05],...
"callback", "startCalculus");
Зарезервируем место для вывода графического решения задачи на графическом окне mainWindow (см. Листинг 23).
framePlot = uicontrol(mainWindow, ...
"style", "frame", ...
"constraints", createConstraints("border", "center"), ...
"backgroundcolor", [0 0 0], ...
"layout", "border",...
"units", "normalized", ...
"position", [0.05 0.02 0.9 0.4]);
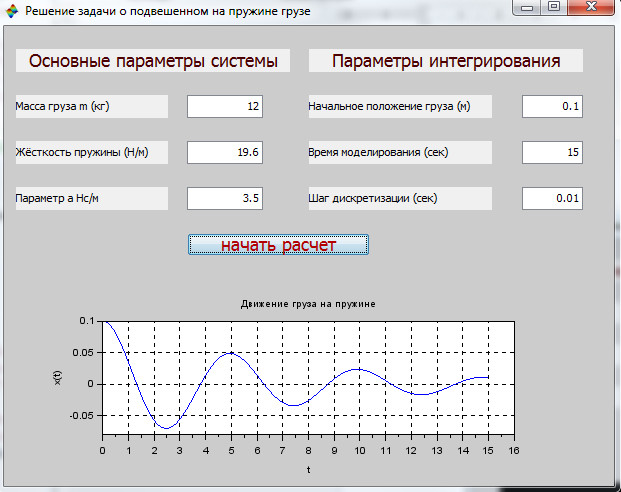
В итоге мы получим графическое окно, на котором расположены необходимые элементы управления, такие что пользователь, не имеющий специальных навыков программирования в среде Scilab, мог бы задавать различные параметры системы, необходимые для численного решения задачи о грузе, подвешенном на пружине (см. рисунок 18)
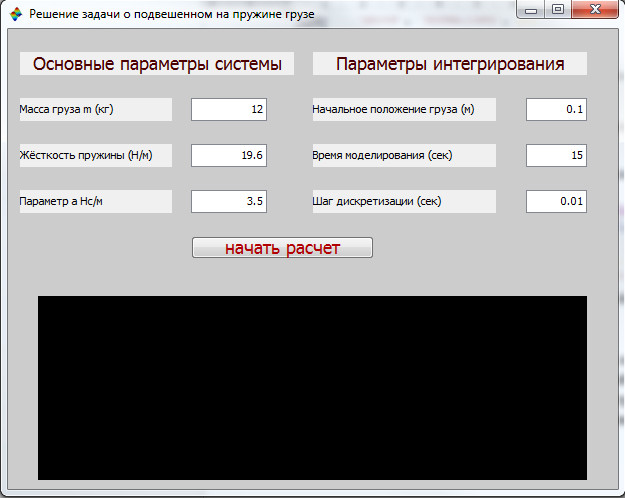
По нажатию на кнопку «начать расчет», происходит вызов пользовательской функции startCalculus(), в которой значения всех полей ввода записываются в переменные
function startCalculus()
g = 9.8;
t0 = 0;
//Считываем параметры
m = evstr(get(mEdit,"String"));
c = evstr(get(cEdit,"String"));
alpha = evstr(get(aEdit,"String"));
x0 = evstr(get(x0Edit,"String"));
d = evstr(get(dEdit,"String"));
Tmax = evstr(get(tmaxEdit,"String"));
....
endfunction
далее формируются входные параметры для функции ode() для решения дифференциального уравнения:
function startCalculus()
....
t = t0:d:Tmax;
//РЕшаем систему ОДУ
z0 = [x0; 0];
z = ode("rk", z0, 0, t, func);
...
endfunction
Численное интегрирование с введёнными параметрами происходит при помощи функции func() за пределами startCalculus()
// Правая часть системы ОДУ
function dz = func(t, z)
dz = zeros(2, 1);
dz(1) = z(2)
dz(2) = -( c*z(1) + alpha*z(2))/m;
endfunction
Вернёмся к startCalculus() и в конце функции осуществим вывод графика движения груза.
function startCalculus()
....
//Рисуем график
clf(framePlot);
a1 = newaxes(framePlot);
a1.axes_bounds = [0 0 1 1];
sca(a1);
plot(t, z(1,:))
xgrid();
xtitle("Движение груза на пружине", "t", "x(t)");
endfunction

Комментарии