Рисуем геометрические объекты в Scilab

Примеры того, как нарисовать сложные фигуры в Scilab

Рассмотрим, как в Scilab строить эллипсы, прямоугольники и произвольные геометрические фигуры.

Прямая линия

Начнём с простого примера построения линии.

Прежде всего, сделаем заготовку графической области, на которой будем рисовать

clc; clf();

plot2d(0,0,-1,"031"," ",[-2,-2,2,2]);
axes = gca();
axes.grid = [2,2];

Квадратная область с сеткой в Scilab

Для того, чтобы нарисовать прямую нам понадобятся две точки и функция \(plot() \).
Итак, для линии, идущей из точки (-1.5, 0) в (1, 1.5) зададим два массива \(х-ов \) и \(у-ков \) соответственно:

xpts = [-1.5 1];
ypts = [0 1.5];

А далее просто построим наш график по заданным точкам (которых всего две):

plot(xpts, ypts);  

line = axes.children.children(1);
//изменим толщину линий на графике  
line.thickness = 2;
  
//изменим цвет линии на графике    
line.foreground = 3;

line.mark_mode = 'on';
line.mark_size = 6;

В итоге получим зелёную полужирную прямую с кругляшами на концах:

Прямая линия в Scilab

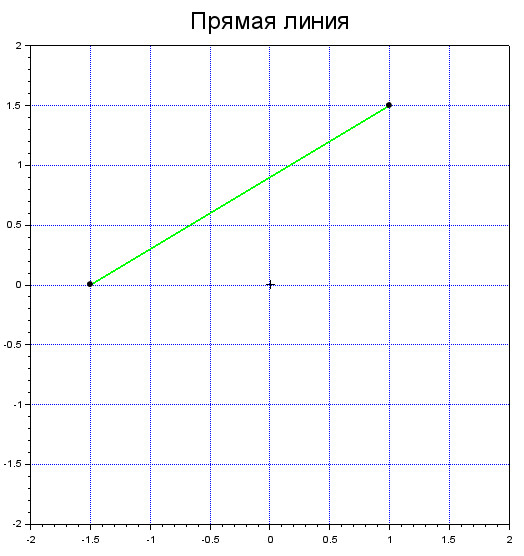
Ломаная линия

Эту линию, конечно, можно продолжить, просто добавив новые элементы в массивы \(xpts \), \(ypts \):

xpts = [-1.5 1 1.5 .5 -1];
ypts = [0 1.5 1 -1.5 -1];

Ломаная линия в Scilab

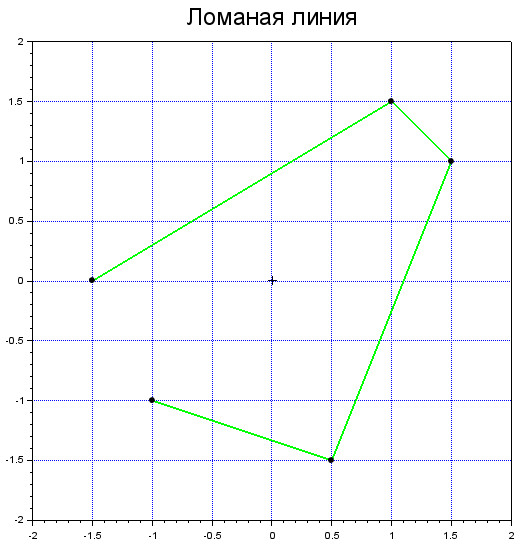
Произвольный многоугольник

Из линии можно сделать многоуголиник, если в массивы координат последними элементами добавить их начальные значения:

xpts = [-1.5 1 1.5 .5 -1 -1.5];
ypts = [0 1.5 1 -1.5 -1 0];

Неправильный многоугольник в Scilab

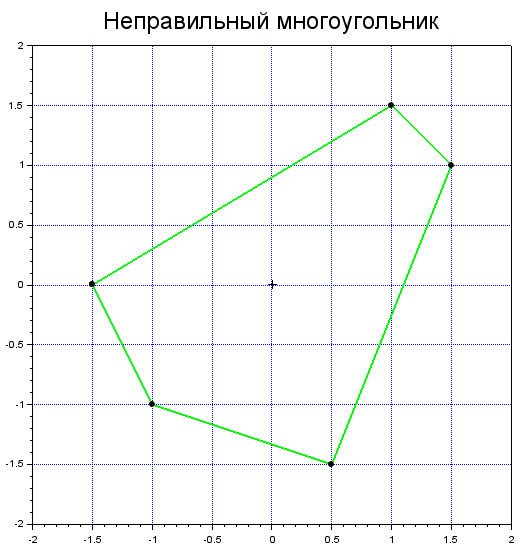
Этот многоугольник можно закрасить, используя способ 1 polyline_style:

line.polyline_style = 5;

Закрашенный многоугольник в Scilab

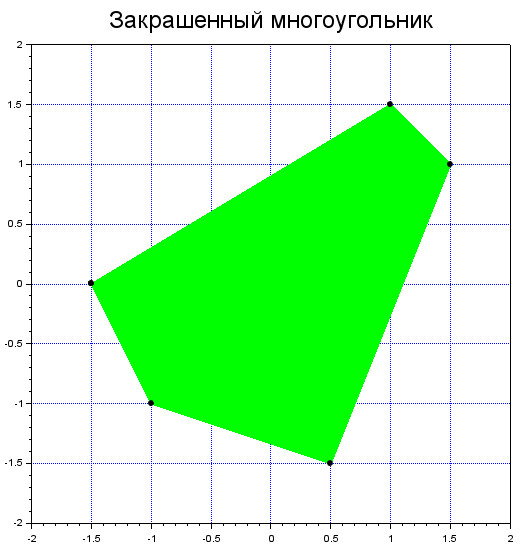
Если же требуется более тонкая настрока цветов, то нуно прибегнуть к способу 2 и вместо polyline_style испольщовать fill_mode и closed. При этом, замыкать ломаную вручную необязательно:

xpts = [-1.5 1 1.5 .5 -1];
ypts = [0 1.5 1 -1.5 -1];
  
line.fill_mode = "on";
line.closed = "on";

//изменим цвет заливки фона  
line.background = 6;  

Закрашенный многоугольник в Scilab

Правильный n-угольник

Теперь, когда мы натренеровались строить и настравивать отображение фигур в Scilab, построим правильный многоугольник, вписанный в единичную окружность.

xpts = [];
ypts = [];

angles = 5;
degreeStep = 2*%pi/angles;

Осталось в цикле вычислисть все \(х-ы\) и \(у-ки\).
Для этого, мы будем \(angles\)-раз крутить вектор, который прикреплён в начале координат, каждый раз увеличивая угол поворота на \(degreeStep\).

Следовательно, интересующие нас координаты - это \(cos() \) и \(sin()\) текущего угла.
А чтобы начинать движение из точки (0, 1), нужно прибавить \( \pi/2 \) к текущему углу:

for j = 1:angles
    xpts(j) =  cos(%pi/2 + degreeStep * j);
    ypts(j) =  sin(%pi/2 + degreeStep * j);
end

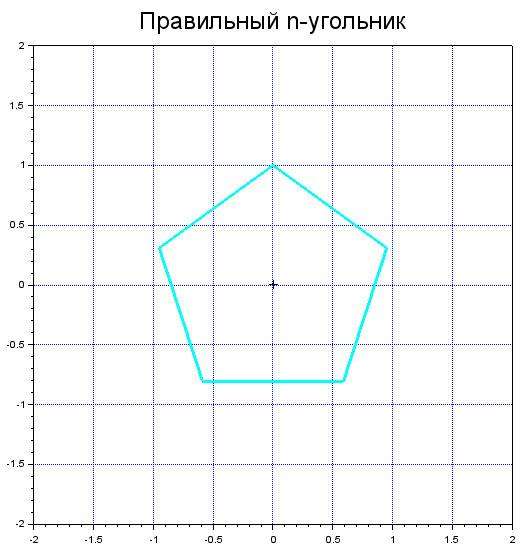
Нарисуем правильный пятиугольник в Scilab, замкнув ломаную и изменим толщину линий и их цвет на графике

plot(xpts, ypts);
line = axes.children.children(1);
line.thickness = 3;
line.foreground = 4;
line.closed = "on";

Правильный многоугольник в Scilab

Эту задачу можно решить и другим способом - с помощью \(xpoly()\)

angles = 8;
degreeStep = 2*%pi/angles;

xpts = sin(degreeStep*(0:angles-1));
ypts= cos(degreeStep*(0:angles-1));

xpoly(xpts,ypts); 
line = gce();
line.thickness = 4;
line.foreground = 6;
line.closed = "on";

Правильный многоугольник с помощью xpoly()

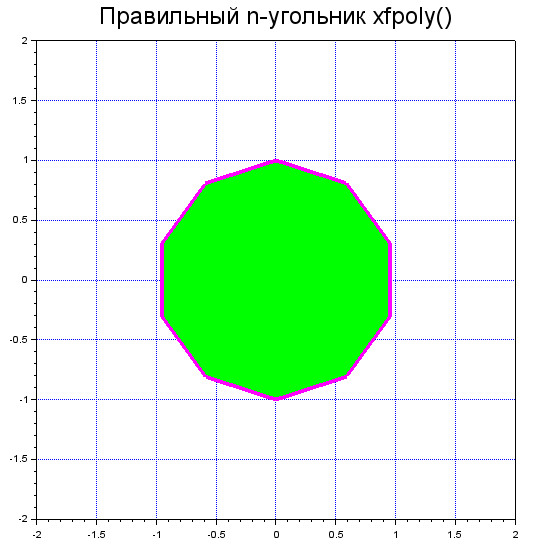
Для того, чтобы нарисовать закрашенный многоугольник, нужно использовать функцию \(xfpoly()\)

angles = 10;
degreeStep = 2*%pi/angles;

xpts = sin(degreeStep*(0:angles-1));
ypts= cos(degreeStep*(0:angles-1));

xfpoly(xpts,ypts); 
line = gce();
line.thickness = 4;
line.foreground = 6;
line.background = 3;
line.closed = "on";

Правильный многоугольник с помощью xfpoly()

Эллипс

Для построения эллипса нужно задать 6 значений:

Значения матрицы эллипса

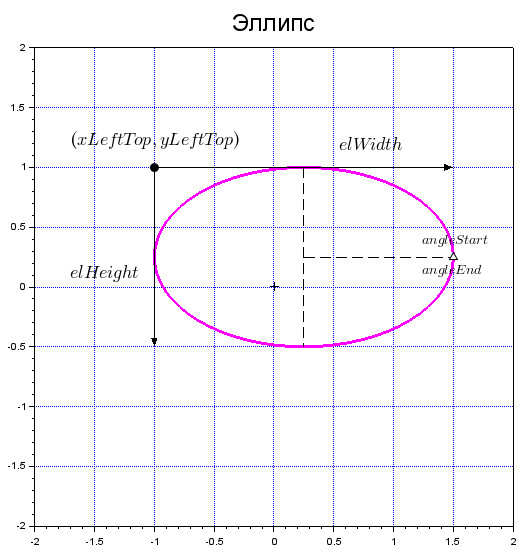
Координаты (xLeftTop, yLeftTop) верхнего левого угла прямоугольника, в который будет вписан эллипс;

Ширину elWidth и Высоту elWidth прямоугольника, в который будет вписан эллипс;

Угол angleStart, откуда будет стартовать дуга эллипса и Угол angleEnd, где дуга остановится.

Для того, чтобы построить изображённый выше эллипс, зададим следующие значения:

xLeftTop = -1;
yLeftTop = 1;

elWidth = 2.5;
elHeight = 1.5;

angleStart = 0;
angleEnd = 360*64;
  
arcs = [xLeftTop; yLeftTop; elWidth; elHeight; angleStart; angleEnd]; 

Сам эллипс по заданным параметрам строится с помощью функции \(xarcs()\):

xarcs(arcs)
  
  
ellips = gce().children;
  
//изменим цвет линии   
ellips.foreground = 6;
//и сделаем её пожирнее    
ellips.thickness = 3;

Сектор

Из эллипса можно строить произвольные сектора, располагая их в желаемом месте на координатной сетке.

Произвольные сектора

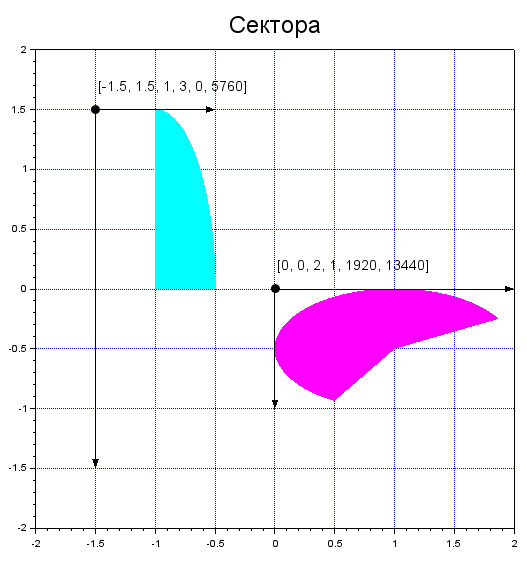
Построим два сектора на основе эллипса с заданными параметрами:

//циановый сектор
xLeftTop = -1.5;
yLeftTop = 1.5;

elWidth = 1;
elHeight = 3;

angleStart = 0;
angleEnd = 90*64;

arcs = [xLeftTop; yLeftTop; elWidth; elHeight; angleStart; angleEnd]; 

xarcs(arcs)
ellips = gce().children;
ellips.fill_mode = "on"
ellips.foreground = 4;
ellips.background = 4;

//маджентовый сектор
xLeftTop = 0;
yLeftTop = 0;

elWidth = 2;
elHeight = 1;

angleStart = 30*64;
angleEnd = 210*64;

arcs = [xLeftTop; yLeftTop; elWidth; elHeight; angleStart; angleEnd]; 

xarcs(arcs)
ellips = gce().children;
ellips.fill_mode = "on"
ellips.foreground = 6;
ellips.background = 6;

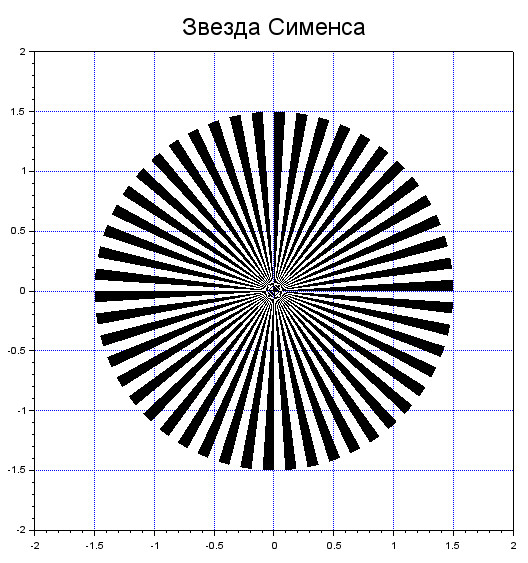
Звезда Сименса

В заключении построим Звезду Сименса изображение, применяемое для проверки остроты зрения (wiki).

Звезда Сименса с 50 лучами

//число секторов  
n = 50;
  
for j = 1:n
   xfarc(-1.5,1.5,3,3,2*j*(180/n)*64,64*(180/n));
end