Обучение нейронной сети
Реализация на Scilab процесса обучения нейронной сети
Соберём уже знакомые функции, которые нам понадобятся:
clc; clf();
function s = sigmoida(V)
x = 1 ./ ( 1 + exp(-V) );
s = roundToDecimal(x, 4);
endfunction
function co = computeNeuronLayer(V, W)
co = W * V;
endfunction
function rd = roundToDecimal(x, m)
rd = round(x * 10^m) / 10^m;
endfunction
Зададим число узлов (нейронов) и слоёв в нашей сети:
rows = 5;
layers = 4;
И сгенерируем нейросеть со случайными матрицами весовых коэффициентов:
[neuralNetwork, weightMatrixes] = createNeuralNetwork(rows, layers);
function [net, matr] = createNeuralNetwork(n, m)
net = zeros(n, m);
net(:, 1) = roundToDecimal( rand(1, n), 2);
matr = list();
for i = 1:m-1
matr($+1) = roundToDecimal( rand(n, n), 2);
end
endfunction
здесь
\(net - \) это матрица нейросети размером \( 5\times 4 \), первый столбец которой - случайный входной вектор, например:
\( net = \begin{pmatrix} 0.21 & 0. & 0. & 0. \\ 0.76 & 0. & 0. & 0.\\ 0. & 0. & 0. & 0.\\ 0.33 & 0. & 0. & 0.\\ 0.67 & 0. & 0. & 0. \end{pmatrix} \)
\(matr - \) гипер-структура list, элементами которой являются весовые матрицы размером \( 5\times 5 \) со случайно сгенерированными значениями, например:
\( weightMatrixes(1) = \begin{pmatrix} 0.29 & 0.65 & 0.61 & 0.57 & 0.12\\ 0.86 & 0.99 & 0.85 & 0.57 & 0.73\\ 0.85 & 0.05 & 0.06 & 0.82 & 0.27\\ 0.53 & 0.75 & 0.83 & 0.06 & 0.55\\ 0.99 & 0.41 & 0.93 & 0.56 & 0.99 \end{pmatrix} \)
Зададим количество итераций \( lim \), массив для сбора результата каждой эпохи \( epoch \), скорость обучения нейросети \( educationSpeed \) и эталонный выход \( vectorOutputEtalon \):
lim = 200;
epoch = [];
educationSpeed = 0.5;
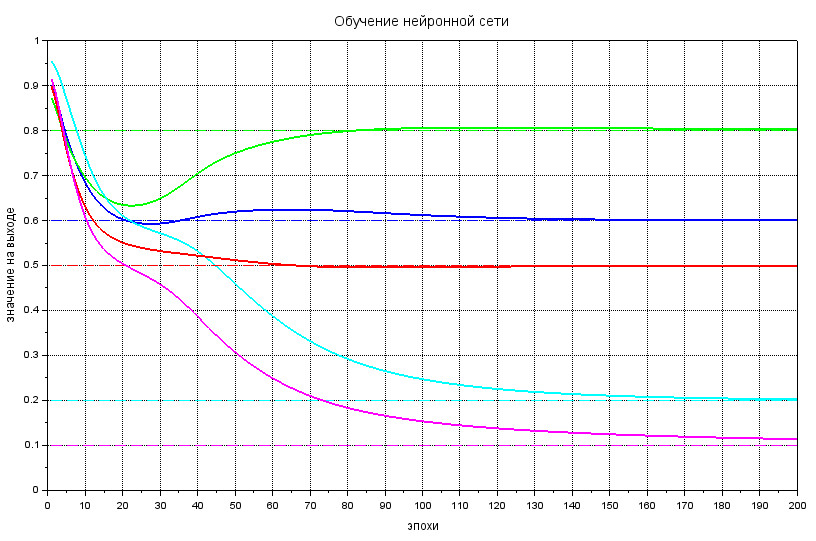
vectorOutputEtalon = [0.6; 0.8; 0.2; 0.5; 0.1];
И с помощью цикла \( for \) проведём обучение неросети на Scilab:
for i=1:lim
// прямое распространение сигнала
for j = 1:layers-1
neuralNetwork(: ,j+1) = sigmoida( computeNeuronLayer(neuralNetwork(: ,j), weightMatrixes(j)) );
end
epoch(:,i) = neuralNetwork(:,layers);
// ОРО и корректировка весов
// ошибка на выходном слое
errorVector = list();
errorVector($+1) = vectorOutputEtalon - neuralNetwork(:, layers);
dW = list();
for k = layers:-1:2
// ошибка на внутренних слоях
Ek = errorVector(1);
errorVector(0) = weightMatrixes(k-1)' * Ek;
j = k - 1;
// поправка для весов
dW(0) = - educationSpeed * Ek .* neuralNetwork(: ,k) .* (1 - neuralNetwork(: ,k)) * neuralNetwork(: ,j)';
// обновление j-ой весовой матрицы
weightMatrixes(j) = roundToDecimal( weightMatrixes(j) - dW(1), 4);
end
end
В первом вложенном цикле происходит прямое распространение сигнала в нейросети - заполнение всех столбцов матрицы \( neuralNetwork \).
Далее в текущий столбец \( epoch \) записывается полученный выходной вектор нейронки, он нам пригодится позже для отслеживания процесса обучения.
После каждого прямого прохода по сети, мы расчитываем ошибку на каждом из слоёв :
- cначала, на выходном,- как разницу эталонного и текущего выхода,
- а далее, во втором вложенном цикле, - на остальных слоях, вплоть до входного.
И, наконец, расчитываем весовую поправку \( dW \) и обновляем коэффициенты весовых матриц \( weightMatrixes \).
Обработка результа тренировки нейронной сети на Scilab
Для того, чтобы не сверять самостоятельно циферки на выходе нейросети с эталонными значениями, выведем график зависимости выходного слоя от эпохи (итерации) обучения:
t = 1:lim;
xtitle("Обучение нейронной сети", "эпохи", "значение на выходе");
xgrid();
legendString = '';
for j = 1:length(vectorOutputEtalon)
plot(t, epoch(j,:) );
gce().children.foreground = j+1;
gce().children.thickness = 2;
plot(t, 0*t + vectorOutputEtalon(j));
gce().children.line_style = 2;
gce().children.foreground = j+1;
end
gca().data_bounds = [0, 0; lim, 1];

Комментарии