ОРО и корректировка весов в нейросети
Ранее мы улучшали поведение простого линейного классификатора и рассмотрели, как по входу и матрицам весов нейросети вычислить её выход.
Теперь предположим, что имеется некий эталоный выход, к которому должен стремиться результат работы нейросети. Для достижения эталона нам потребуется что-то перенастраивать в сети. Это будут весовые коэффициенты.
Выясним, как мы будем обновлять матрицы весов.
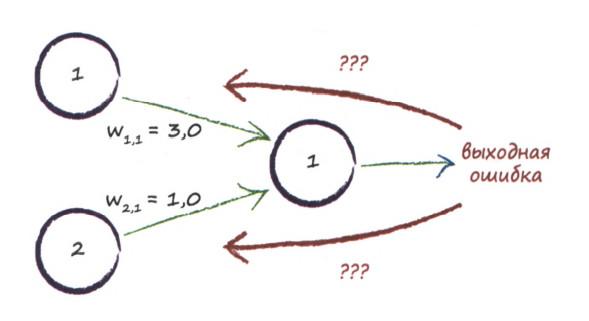
Обратное распространение ошибки в нейронной сети
Воспользуемся методом ОРО, пропорционально распределяя ошибку между имеющимися узлами:
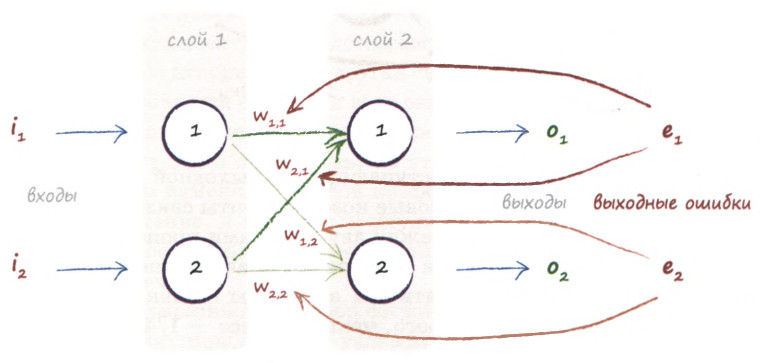
Определим ошибку на выходном слое \( e^{О}\), как разность между эталонным значением \( t_{i}\) и полученным \( o_{i}\) на выходе нейросети :
\( e^{О}_{i} = t_{i} - o_{i}\)
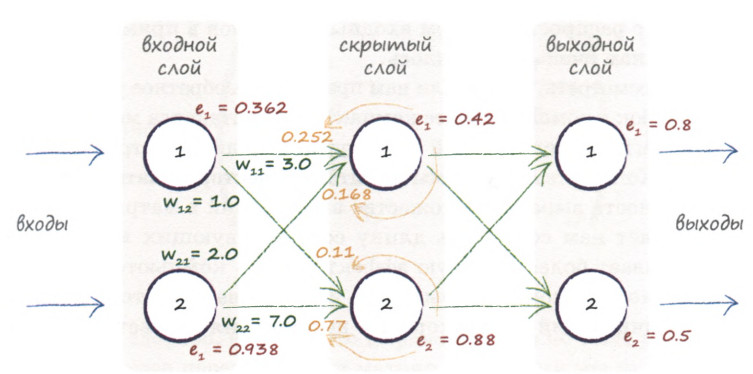
Тогда, глядя на рисунок выше, заключим, что ошибка \( e^{О}_{1}\) распределяется пропорционально весам \( w_{11}\) и \( w_{21}\), а ошибка \( e^{О}_{2}\) должна распределяться пропорционально весам \( w_{12}\) и \( w_{22}\).
Запишем эти доли в явном виде:
\( e^{O}_{1} = \displaystyle\frac {w_{11}}{w_{11} + w_{21}}; \quad e^{O}_{2} = \displaystyle\frac {w_{12}}{w_{12} + w_{22}}, \)
Итак, на основе отклонения текущего выхода от эталонного, мы будем обновлять весовые коэффициенты во всей нейросети, двигаясь с конца к её началу.
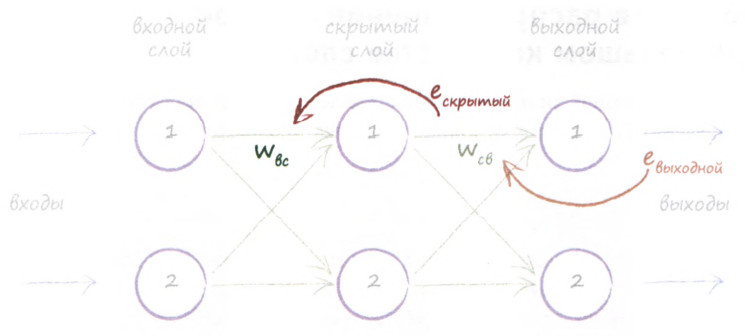
Но если сначала мы использовали ошибку выходного слоя, то какую ошибку использовать для узлов скрытого слоя? Ведь мы не можем указать очевидную ошибку для узла в таком слое.
Разберёмся, как определить ошибку для скрытого узла.
Ошибка скрытого слоя
Мы можем воссоединить ошибки, распределенные по связям следующим образом: ошибка на первом скрытом узле \( e^{H}_{1} \) представляет собой сумму ошибок, распределенных по всем связям, исходящим из этого узла в прямом направлении:
\( e^{H}_{1} = e^{O}_{1} \cdot \frac {w_{11}}{w_{11} + w_{21}} + e^{O}_{2} \cdot \frac {w_{12}}{w_{12} + w_{22}}, \)
или как показано на иллюстрации ниже:
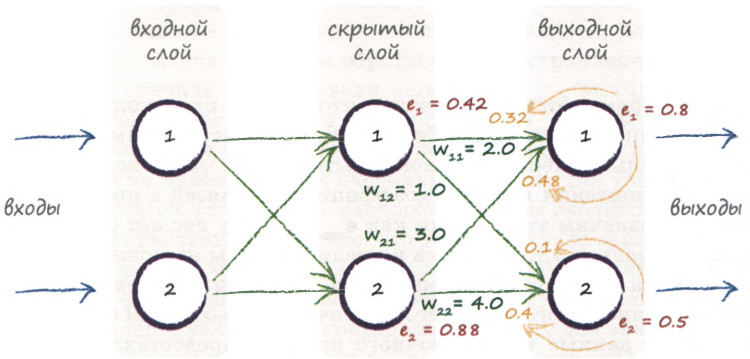
Применять данную методику мы будем до тех пор, пока не доберёмся до входного слоя:
Векторизация метода ОРО в нейросети
Опять, так как Scilab - матричный язык, адаптируем поэлементный процесс обратного распространения ошибки в нейросети под удобный нам.
Зададим эталонный вектор \( V_{e}\), тогда ошибка \( E_O\) на выходном слое \( O\) считается самым простым способом:
\( E_O = V_{e} - O \)
Ошибка \( E_H \) на скрытом слое \( H\) будет считаться с учетом вклада каждого узла следующим образом:
\( E_H = \begin{pmatrix} \frac {w_{11}}{w_{11} + w_{21}} & \frac {w_{12}}{w_{12} + w_{22}} \\ \frac {w_{21}}{w_{21} + w_{11}} & \frac {w_{22}}{w_{22} + w_{12}} \end{pmatrix} \cdot E_o \)
Здесь \( w_{ij} \) - элементы матрицы \( W_{HO} \), задающей веса для слоёв выходной-скрытый.
Это выражение можно переписать в более простом виде, отказавшись от знаменателей в первом множителе. Тогда получим связь с весовой матрицей на текущем шаге:
\( E_H = \begin{pmatrix} w_{11} & w_{12} \\ w_{21} & w_{22} \end{pmatrix} \cdot E_O \)
Итак, ошибка \( E_H \) скрытого вычисляется с учётом ошибки \(E_O\) выходного слоя и матрицы \( W_{HO} \):
\( E_H = W_{HO}^T \cdot E_O\)
Аналогично, для входного слоя ошибка \( E_I \) будет вычисляться с учётом ошибки \(E_H\) предыдущего слоя в связи с матрицей \( W_{IH} \), определяющей веса входной-скрытый слоёв:
\( E_I = W_{IH}^T \cdot E_H\)
Обновление весовых коэффициентов
Для обновления весовых коэффициентов мы воспользуемся методом градиентного спуска (подробнее в (1)).
При подсчёте ошибки на каждом из слоёв, будем немного корректировать весовые коэффициенты соответвующей весовой матрицы на величину \( \Delta w \), которая на векторно-матричном языке может быть представлена как:
\( \Delta w = - \alpha \cdot E_k \cdot O_k \cdot (1 - O_k) \cdot O^T_j, \)
где
\(\alpha - \) скорость обучения нейронной сети \(\alpha \in (0,1) \),
\(E_k - \) ошибка текущего слоя (вектор столбец),
\(O_k - \) текущий слой (вектор-столбец),
\(O^T_j - \) предыдущий слой (вектор-столбец).
А обновлённая матрица весов примет вид:
\( W^{new} = W^{cur} - \Delta w \)
Осталось лишь собрать всё в программный код обучения нейросети 😁
Данная статья создана на основе чудесной книги(1) с реализацией автором приведённых примеров на Scilab.

Комментарии