Простейшая нейронная сеть на Scilab
Ранее был рассмотрен вопрос настройки линейного классификатора, как заготовки для понимания принципов машинного обучения.
В даннном материале попробуем углубиться в тему и рассмотрим, как распространяется импульс в искусственной нейронной сети.
Искусственная нейросеть из 3-х слоёв
На иллюстрации ниже представлены три слоя нейронки, каждый из которых включает три искусственных нейрона, или узла. Как нетрудно заметить, здесь каждый узел соединен с каждым из узлов предшествующего и последующего слоев.
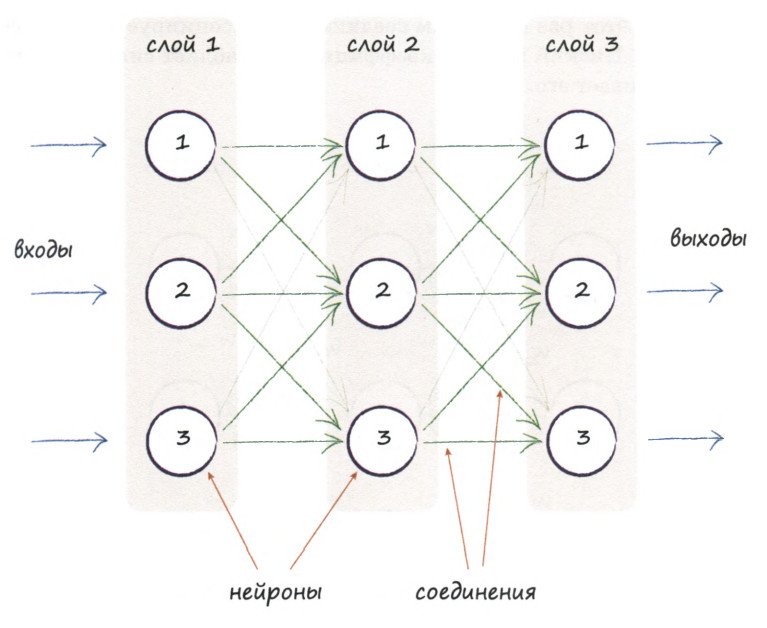
Каждый нейрон принимает сигнал, неким образом его обрабатывает и передаёт дальше.
Функция активации
В качестве правила, по которому происходят метаморфозы сигнала внутри нейрона мы будем использовать логистическую функцию вида:
\( \sigma = \displaystyle\frac{1}{1+e^{-x}} \quad (1) \)
Функция (1) называется ещё и сигмоидой, она очень популярна в области искусственного интеллекта благодаря своей гладкости и простоте расчётов.
Кроме того, выбранная функция хороша ещё и тем, что если комбинированный сигнал недостаточно сильный, то сигмоида подавляет выходной сигнал, в противном случае функция возбуждает нейрон.
Итак, структура сети определена, функция активации выбрана, осталось определить, каким образом наша сеть будет обучаться.
Весовые коэффициенты
Величиной, которую мы будем регулировать на основе тренировочных данных, является сила связи между узлами.
При этом, будем считать, что низкий весовой коэффициент ослабляет сигнал, высокий - усиливает его. Как только сеть научится улучшать свои выходные значения путем уточнения весовых коэффициентов, некоторые веса обнулятся или станут близкими к нулю, что означает фактический разрыв связи.
Определим для каждого соединения его вес:
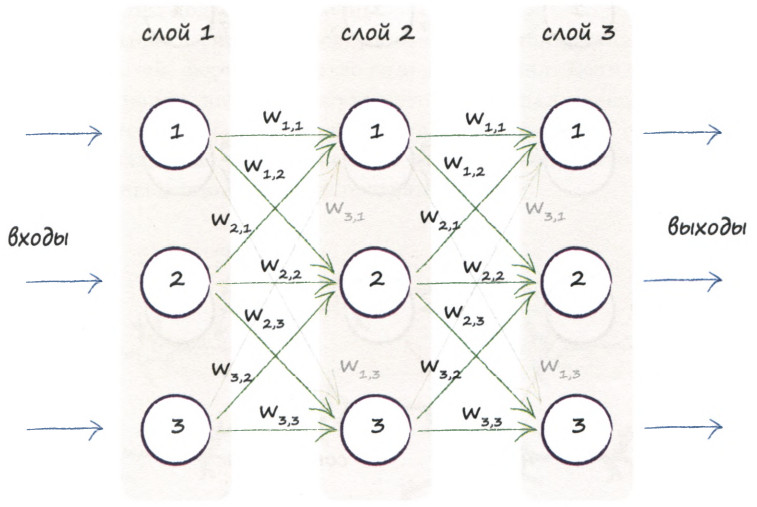
Посмотрим внимательно на схему распределения весов.
Заметим, что весовой коэффициет \( w_{i,j} \) соответствует сигналу, передаваемому от \( i-го\) узла текущего слоя к \( j-му\) узлу следующего слоя.
Например к 1-му нейрону 2-го слоя подходят три стрелочки: от 1-го, 2-го и 3-го нейронов 1-го слоя, с весами \( w_{1,1}, w_{2,1}, w_{3,1} \) соотвественно.
Согласно общепрянотой терминологии, мы будем называть слои следуюющим образом:
Первый слой узлов будем называть \(входным\);
Последний слой - \(выходным\);
А все слои между ними - \(скрытыми\).
Прямое распространение сигнала в нейронной сети
Приступим к пошаговой реализации распространения сигнала в нашей нейросети.
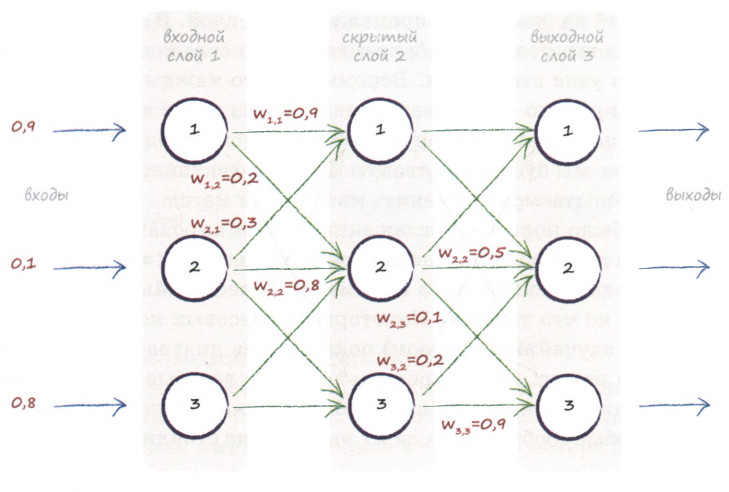
Входной слой
Зададим вектор входных сигналов:
\( I = \begin{pmatrix} 0.9 \\ 0.1 \\ 0.8 \end{pmatrix} \)
С первым слоем все просто - никаких вычислений.
Первый слой узлов имеет единственное назначение - представлять входные сигналы. Таким образом, во входных узлах функция активации к входным сигналам не применяется.
Хорошо. что Scilab - матрично-ориентированный язык, поэтому задание вектора входного сигнала будет выглядеть следующим образом:
vectorInput = [.9; .1; .8];
disp("Входной вектор", vectorInput);
Скрытый слой
Следующий на очереди - промежуточный слой.
Для каждого нейрона этого слоя нужно будет посчитать свой вход, к нему применить функцию активации и подать результат на выход нейрона.
Вход скрытого слоя
Предположим, весовые коэффициенты для связи между входным и скрытым слоями заданы следующим образом:
\( w_{1,1}=0.9, w_{2,1}=0.3, w_{3,1}=0.4 \)
\( w_{1,2}=0.2, w_{2,2}=0.8, w_{3,2}=0.2 \)
\( w_{1,3}=0.1, w_{2,3}=0.5, w_{3,3}=0.5 \)
Индексы весовых коэффициентов показывают откуда куда идут стрелочки.
Соответственно, чтобы вычислить вход 1-го нейрона скрытого слоя \( H_{i}(1) \), необдимо взять сумму весов \( w_{1,1}=0.9, w_{2,1}=0.3, w_{3,1}=0.4 \) (стрелочки идут от 1-го, 2-го и 3-го нейрона входного слоя к 1-му нейрону скрытого), умноженных на соответсвующий выход предыдущего слоя:
\( H_{i}(1) = w_{1,1}\cdot I(1) + w_{2,1}\cdot I(2) + w_{3,1}\cdot I(3) = 0.9\cdot0.9 + 0.3\cdot0.1 + 0.4\cdot0.8=1.16 \)
Аналогично вычислим вход 2-го и 3-го нейронов скрытого слоя \( H_{i}(2), H_{i}(3) \):
\( H_{i}(2) = w_{1,2}\cdot I(1) + w_{2,2}\cdot I(2) + w_{3,2}\cdot I(3) = 0.2\cdot0.9 + 0.8\cdot0.1 + 0.2\cdot0.8=0.42 \)
\( H_{i}(3) = w_{1,3}\cdot I(1) + w_{2,3}\cdot I(2) + w_{3,3}\cdot I(3) = 0.1\cdot0.9 + 0.5\cdot0.1 + 0.6\cdot0.8=0.62 \)
Кажется, имеется некоторая закономерность в производимых действиях 😉. Действительно, если из весовых коэффициентов сформировать матрицу:
\( W_{IH} = \begin{pmatrix} w_{1,1} & w_{2,1} & w_{3,1} \\ w_{1,2} & w_{2,2} & w_{3,2} \\ w_{1,3} & w_{2,3} & w_{3,3} \\ \end{pmatrix} \)
То вход скрытого слоя можно отыскать простым матричным умножением:
\( H_{i} = W_{IH}\cdot I \quad (2) \)
Зададим матрицу весов входной-скрытый на Scilab:
matrixInputHidden = [0.9 0.3 0.4; 0.2 0.8 0.2; 0.1 0.5 0.6];
disp("Матрица входной-скрытый", matrixInputHidden);
А чтобы посчитать вход скрытого слоя напишем функцию согласно (2):
function co = computeNeuronLayer(V, W)
co = W * V;
endfunction
vectorHidden = computeNeuronLayer(vectorInput, matrixInputHidden);
disp("Вход скрытого", vectorHidden);
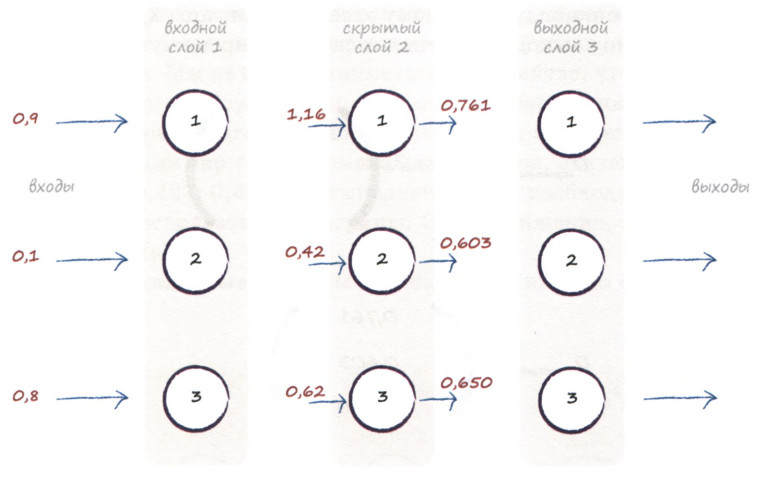
Отобразим входные сигналы для скрытого слоя на диаграмме.
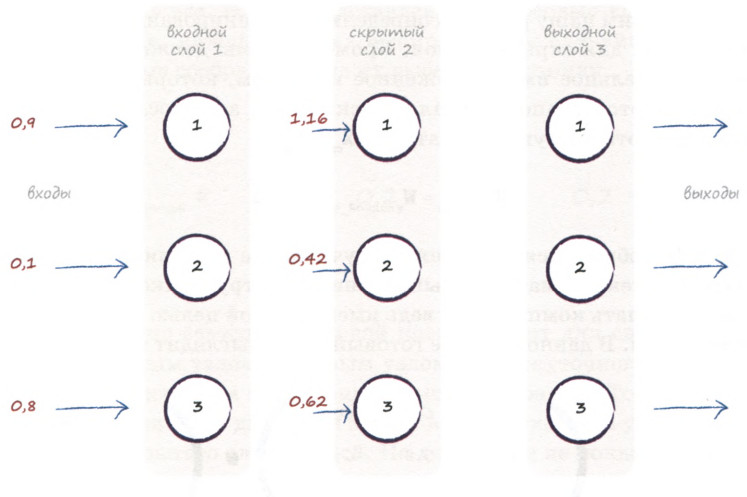
Итак, мы сформировали вектор-столбец входных сигналов скрытого слоя:
\( H_i = \begin{pmatrix} 1.16 \\ 0.42 \\ 0.62 \end{pmatrix} \)
Пока что все хорошо, но нам еще остается кое-что сделать.
Выход скрытого слоя
Как вы помните, чтобы отклик слоя на входной сигнал как можно лучше имитировал аналогичный реальный процесс, мы должны применить к узлам функцию активации. Так и поступим:
\( H_{o} = \sigma(H_i) \quad (3) \)
Применяя сигмоиду ко входу скрытого слоя, получим его выход:
\( H_o = \begin{pmatrix} 0.761 \\ 0.603 \\ 0.650 \end{pmatrix} \)
В Sciab нет встроенной функции сигмоиды, поэтому напишем свою:
function s = sigmoida(V)
x = 1 ./ ( 1 + exp(-V) );
s = roundToDecimal(x, 3);
endfunction
Заметьте, что в функции присутствует "./" - это поэлементное деление в Scilab, так как в качестве параметра мы передаём вектор 😎
И применим её ко входу скрытого слоя:
vectorHidden = sigmoida(vectorHidden)
disp("Выход скрытого", vectorHidden)
Функция \( roundToDecimal(\cdot, \cdot); \) нам нужна, чтобы округлять результат до нужного знака после запятой. Выглядит она предельно просто:
function rd = roundToDecimal(x, m)
rd = round(x * 10^m) / 10^m;
endfunction
Выходной слой
Для выходного слоя задача прохождения сигнала (О чудо!) ничем не отличается от предыдущего шага!
Перелесть проделанных на шаге 2 действий в том, что сколько бы слоёв ни было в нашей сети, вход каждого из них будет вычисляться путём умножения соответствующей матрицы весов и на выход предыдущего слоя, а его выход - путём применениия функции активации к полученному результату 👏
Итак, по аналогии со скрытым слоем, зададим матрицу весовых коэффициентов скрытый-выходной:
\( W_{HO} = \begin{pmatrix} w_{1,1} & w_{2,1} & w_{3,1} \\ w_{1,2} & w_{2,2} & w_{3,2} \\ w_{1,3} & w_{2,3} & w_{3,3} \\ \end{pmatrix} = \begin{pmatrix} 0.3 & 0.7 & 0.5 \\ 0.6 & 0.5 & 0.2 \\ 0.8 & 0.1 & 0.9 \\ \end{pmatrix} \)
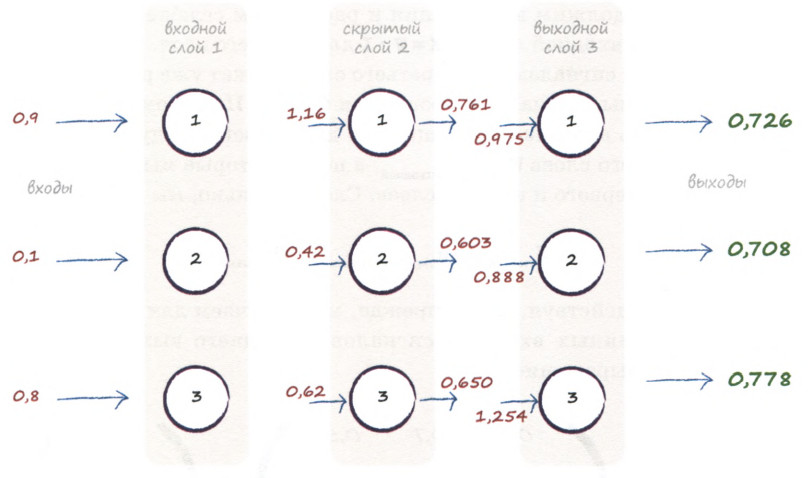
И посчитаем вход выходного слоя:
\( O_i = W_{HO}\cdot I_o = \begin{pmatrix} 0.3 & 0.7 & 0.5 \\ 0.6 & 0.5 & 0.2 \\ 0.8 & 0.1 & 0.9 \\ \end{pmatrix} \cdot \begin{pmatrix} 0.761 \\ 0.603 \\ 0.650 \end{pmatrix} = \begin{pmatrix} 0.975 \\ 0.888 \\ 1.254 \end{pmatrix} \)
Все, что нам остается, это применить сигмоиду к \( O_i \)
\( O_o = \sigma \begin{pmatrix} 0.975 \\ 0.888 \\ 1.254 \end{pmatrix} = \begin{pmatrix} 0.726 \\ 0.708 \\ 0.778 \end{pmatrix} \)
И, наконец, мы получили сигналы на выходе нейронной сейти:
Проделаем те же действия в Scilab:
matrixHiddenOutput = [0.3 0.7 0.5; 0.6 0.5 0.2; 0.8 0.1 0.9];
disp("Матрица скрытый-выходной", matrixHiddenOutput)
vectorOutput = computeNeuronLayer(vectorHidden, matrixHiddenOutput);
disp("Вход выходного", vectorOutput)
vectorOutput = sigmoida(vectorOutput)
disp("Выход выходного", vectorOutput)
Итак, нам удалось успешно описать прямое распространение сигналов по нейросети, т.е. определить величину выходных сигналов при заданных величинах входных сигналов.
Цикл для прямого распределения сигнала в нейронке
Рассмотренный пошаговый метод, конечно, имеет место быть, но при увеличении числа слоёв и нейронов в слое, нам придётся многократно повторять одни и те же действия. Поэтому облегчим себе жизнь с помощью циклической обработки однотипных действий.
Соберём все собственные функции:
clc;
function rd = roundToDecimal(x, m)
rd = round(x * 10^m) / 10^m;
endfunction
function s = sigmoida(V)
x = 1 ./ ( 1 + exp(-V) );
s = roundToDecimal(x, 3);
endfunction
function co = computeNeuronLayer(V, W)
co = W * V;
endfunction
Зададим желаемое число нейронов и слоёв в нейросети:
rows = 3;
layers = 3;
И сгенерируем заготовку для сети:
neuralNetwork = zeros(rows, layers);
\( neuralNetwork = \begin{pmatrix} 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{pmatrix} \)
Первый столбец в матрице сети- это входной вектор \( I \). Зададим первый стобец матрицы, как в разобранном примере:
neuralNetwork(:, 1) = [.9; .1; .8];
\( neuralNetwork = \begin{pmatrix} 0.9 & 0 & 0\\ 0.1 & 0 & 0\\ 0.8 & 0 & 0 \end{pmatrix} \)
Далее необходимо задать матрицы весов. Чтобы с ними было удобно работать, объединим матрицы в гипер-структуру - список \( list(); \) и зададим две матрицы \( W_{IH}, W_{HO} \), как в примере выше:
weightMatrixes = list();
weightMatrixes(1) = [0.9 0.3 0.4; 0.2 0.8 0.2; 0.1 0.5 0.6];
weightMatrixes(2) = [0.3 0.7 0.5; 0.6 0.5 0.2; 0.8 0.1 0.9];
Теперь элемент списка \( weightMatrixes(); \) - это целиком весовая матрица:
\( \begin{matrix} weightMatrixes(1) = \begin{pmatrix} 0.9 & 0.3 & 0.4\\ 0.2 & 0.8 & 0.2\\ 0.1 & 0.5 & 0.6 \end{pmatrix} & weightMatrixes(2) = \begin{pmatrix} 0.3 & 0.7 & 0.5\\ 0.6 & 0.5 & 0.2\\ 0.8 & 0.1 & 0.9 \end{pmatrix} \end{matrix} \)
Осталось лишь запустить цикл вычисления скрытого и выходного слоёв.
Каждый новый слой (столбец матрицы neuralNetwork) - это результат применения сигмоиды к произведению текущего слоя (столбца) и соответствующей весовой матрицы:
for j = 1:layers-1
neuralNetwork(: ,j+1) = sigmoida( computeNeuronLayer(neuralNetwork(: ,j), weightMatrixes(j)) );
end
Убедимся, что результат совпадает с посчитанным поэтапно:
disp(neuralNetwork);
\( neuralNetwork = \begin{pmatrix} 0.9 & 0.761 & 0.726\\ 0.1 & 0.603 & 0.708\\ 0.8 & 0.65 & 0.778 \end{pmatrix} \)
Отлично! Результат совпал. Можно двигаться дальше.
Далее мы приступим к разбору метода обратного распределения ошибки и корректировки весов 🤓
Данная статья создана на основе чудесной книги(1) с реализацией автором приведённых примеров на Scilab.

Комментарии