Решение дифференциального уравнения 2-ой степени в Xcos.
Дифференциальные уравнения первой степени являются простейшими составляющими математических моделей и используются, чаще всего, для нормализации дифференциальных уравнений высших порядков.
Мы остановимся на рассмотрении ОДУ 2-ой степени и двух подходах поиска его решения посредством составления блок-схем Xcos. Первый подход заключается в последовательном интегрировании правой части дифференциального уравнения, то есть, использования двух блоков-интеграторов.
Способ 1: последовательное интегрирование
Рассмотрим дифференциальное уравнение второго порядка с заданными начальными условиями:
\( y''-0.5y'+y=0.2x-1.3, y(0)=-1, y'(0)=1 \) (1)
Как и в случае с д.у. первой степени, уравнение (1) необходимо привести к виду, где слева от знака «равно» будет наивысшая производная, а справа – остальные слагаемые, то есть к следующему виду:
\( y''=0.5y'-y+0.2x-1.3 \) (2)
И в последующем рассмотреть сумму, стоящих справа от знака «равно» слагаемых, при этом, приняв каждую из производных y, как интеграл от исходной суммы. То есть, условно произвести последовательную замену и подстановку производных и воспользоваться принципом, что \( \int{y''}=y'\), а \( \int{\int{y''}}=\int{y'}=y\). Рассмотрим данный процесс на нашем примере.
Чтобы составить блок-схему дифференциального уравнения второй степени (2) нужно:
Добавить блок сумматора BIGSOM_f. Во внутренних параметрах данного блока указать вектор знаков слагаемых. В нашем случае справа стоят 4 слагаемых, знак первого слагаемого «+», далее «-», потом опять «-» и снова «+», поэтому во внутреннем параметре Input ports signs нужно указать [1;-1;1;-1];
Добавить два интегратора (так как уравнение 2-й степени), указав соответствующие начальные условия из (1) во внутренних параметрах каждого из блоков INTEGRAL_f;
Соединённых последовательно блок сумматора и интеграторов. На данном этапе должна получиться схема, изображённая на рис. 33.
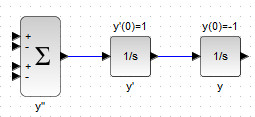
Далее необходимо добавить в сумму слагаемые \( y \) и \( y' \) с соответствующими множителями, как показано на рис. 34. Здесь первые два слагаемых в блоке сумматора образуют сумму \( 0.5y'-y\)
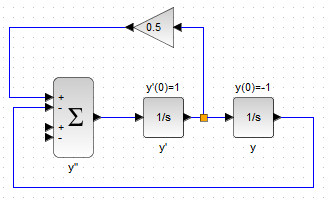
В сумматоре остались два свободных положительных входа. На них нужно подать независимую переменную , усиленную блоком GAINBLK_f и константу
см. рис.35.
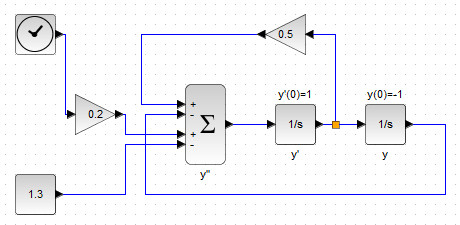
Для вывода графической информации, используйте блоки MUX, CMSCOPE, END и CLOCK_c с уже известным функционалом.
Итоговая блок-схема для поиска решения ОДУ с заданными начальными условиями изображена на рисунке 36.
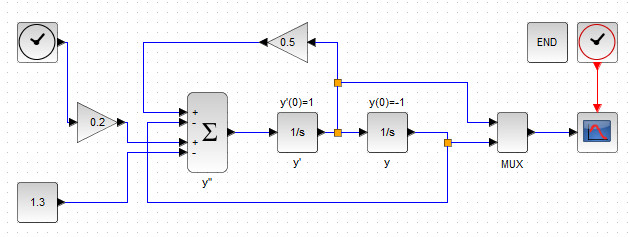
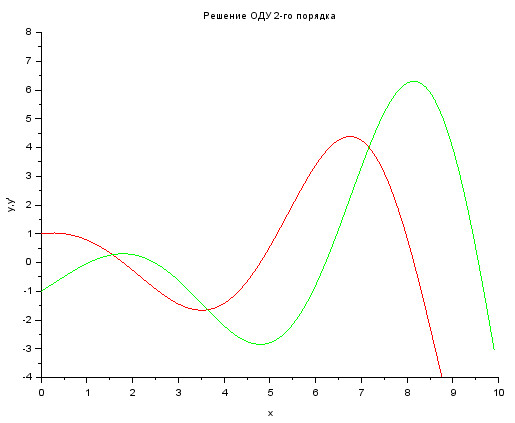
Моделирование проводилось на временном отрезке [0;10] с шагом дискретизации 0.1. На рис. 37. Представлены графики: зелёным цветом - искомой функции \( y \) и красным - её производной \( y' \).
Мы разобрали на примере один из способов численного интегрирования в Xcos дифференциальных уравнений степени, выше 1 с заданными начальными условиями. Обозначим основные принципы рассмотренного подхода последовательного интегрирования:
Приведение дифференциального уравнения n-ой к виду, когда слева от знака «равно» находится только производная;
Использование блока TIME_f для подачи независимой переменной на вход функциональных блоков;
Последовательное подключение блоков INTEGRAL_f для обозначения производных порядка до (n-1) искомой функции;
Задание начальных условий в соответствующих блоках-интеграторах;
Задание отрезка интегрирования во внутренних параметрах блока END, начальной точки и шага дискретизации в блоке CLOCK_c;
Возможность выбора численного метода поиска решения дифференциального уравнения в настройкам параметров интегрирования.

Комментарии