Решение дифференциального уравнения 1-ой степени в Xcos
Перейдём, наконец к визуальному моделированию динамических систем в Xcos. Не секрет, что различные механические, физические, экономические и многие другие системы реальной жизни описываются в виде математических моделей на основе дифференциальных уравнений.
Рассмотрим порядок решения задачи Коши для дифференциального уравнения первого порядка с заданным начальным условием:
\( y'-4cos(3x)=1, y(0)=-2 \) (1)
Аналитическое решения данного уравнения имеет вид:
\( y=x+\frac{4}{3}sin(3x)-2 \) (2)
Перейдём к построению блок-схемы в редакторе Xcos. Наша блок-схема будет состоять из двух частей: части, моделирующей найденное аналитическое решение задачи Коши (2) и части, отвечающей за численное интегрирование исходного дифференциального уравнения с заданными начальными условиями (1). Мы ни в коем случае не желаем запутать читателя или усложнить схему. Целью построения блок-схемы из двух является демонстрация идентичности решений – аналитического и численного.
Для моделирования блока аналитического решения нам понадобится единственный новый блок 
с палитры «Источники сигналов и воздействий» , необходимый непосредственно для генерации сигнала. Данный блок имеет только один регулярный выход и не имеет внутренних параметров; он необходим для подачи временных отсчетов, синхронизированных в соответствии с параметрами блоков CLOCK_c и END.
Итак, исходя из того, что моделируемое уравнение (2) имеем три слагаемых, нам понадобится блок BIGSOM_f, два входа которого будут положительными, а один, соответствующий константе «-2» - отрицательным. Сложносочинённым в моделируемом уравнении представляется второе слагаемое \( \frac{4}{3}sin(3x) \), которое представляет из себя произведение константы \( \frac{4}{3} \) и синусоиды \( sin(\cdot) \), причём, аргумент синусоиды сам представляет собой увеличенный в три раза \( x \). Осуществлять вывод графиков моделируемых уравнений будет CMSCOPE. Блок-схема уравнения (2) представлена на рис. 30. Обратите внимание на использование блока GAINBLK_f, усиливающего исходный сигнал в три раза, а затем подающий его в функцию синуса.
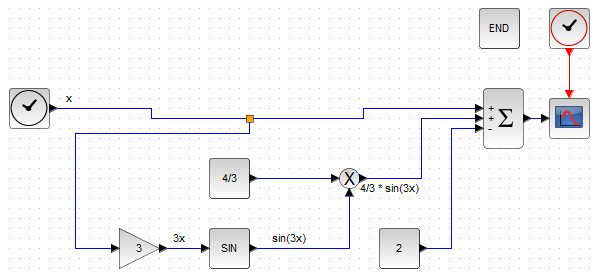
Теперь перейдём к реализации блок-схемы дифференциального уравнения первой степени в среде визуального моделирования Xcos.
Первое, что необходимо сделать – это привести дифференциальное уравнение к интегрируемому виду, где слева от знака «равно» стоит производная, а справа – остальные слагаемые. В рассматриваемом примере, уравнение (1) преобразуется к виду:
\( y'=1+4cos(3x) \) (3)
Далее, нам необходимо собрать из блоков Xcos правую часть уравнения (3), состоящую из двух слагаемых, а результат направить на блок интегрирования 
, который располагается на палитре «Системы с непрерывным временем». У блока INTEGRAL_f всего один внутренний параметр Initial state, в котором указывается значение в начальный момент времени. В нашем случае начальные условия заданы в (1) и имеют вид \( y(0)=-2 \), а значит, параметр Initial state блока INTEGRAL_f нужно установить равным -2. На выходе у блока-интегратора будет результат интегрирования правой части д.у. с н.у. (1), то есть численное решение исходной задачи Коши для дифференциального уравнения первой степени.
Итоговая блок-схема, выводящая аналитическое и численное решения на одну систему координат, представлена на рисунке 31.
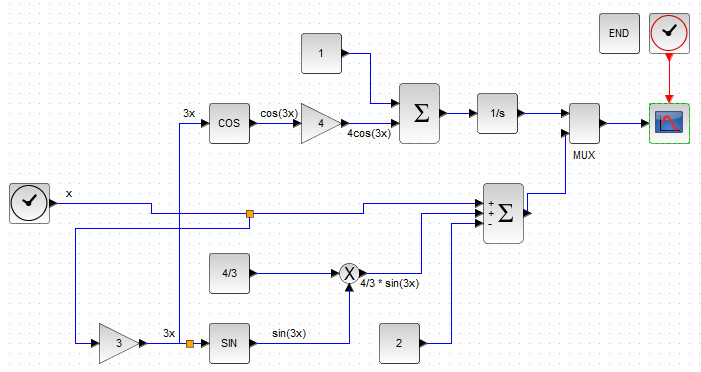
Моделирование проводилось на временном отрезке [0;5] с шагом дискретизации 0.1. Результат моделирования представлен на рис. 32.
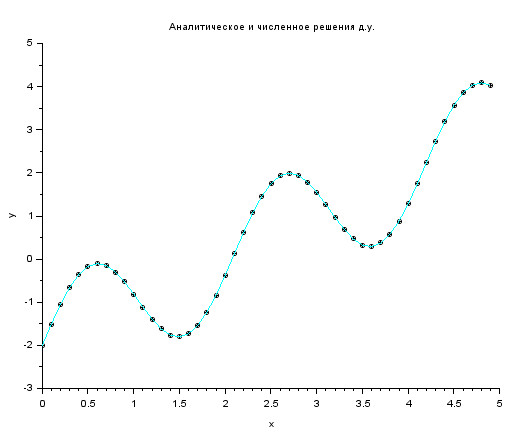
Итак, нами рассмотрен подход к решению задачи Коши для ОДУ 1-ой степени.
Основные принципы данного подхода следующие:
Приведение дифференциального уравнения к виду, когда слева от знака «равно» находится только производная;
Использование блока TIME_f для подачи сигнала на вход функциональных блоков;
Использование блока INTEGRAL_f для поиска численного решения дифференциального уравнения;
Задание отрезка интегрирования во внутренних параметрах блока END, начальной точки и шага дискретизации в блоке CLOCK_c;
Возможность выбора численного метода поиска решения дифференциального уравнения в настройкам параметров интегрирования.
Комментарии