Математическая модель управления численностью популяции в Xcos
Обратимся к рассмотренной в статье модели Хищник-Жертва, предложенной Лотки-Волтерра и попытаемся ею поуправлять, то есть введём управление F в систему, так, что она преобразуется к виду:
(1)\begin{cases} \dot{x}=ax-bxy+F(t)x\\ \dot{y}=dxy-cy\\ \end{cases}
Итак, судя по виду системы (1), управлять мы будем численностью жертв \( x \) в каждый момент времени \( t \). Функция \( F(t) \)в данном случае может быть рассмотрена как индикатор смертности жертвы, то есть значение \( F(t) \leq 0 \) свидетельствует об убыли особей-жертв, значение \( F(t) = 0 \) означает, что жертвы смогли избежать гибели в момент времени .
Рассмотрим в качестве управляющего закона следующий:
(2) \[ F(t) = \begin{cases} sin(\frac{x}{2}), &\quad \text{если} \; x < x_{min}\\ \text{u = const,} &\quad \text{если} \; x > x_{max} \\ \end{cases} \]
Систему (2) можно интерпретировать следующим образом:
при достаточно высокой популяции жертв, их смертность примерно одинакова;
при малом же количестве добычи, вероятность ею полакомится снижается.
Отметим, что в системе без управления присутствует состояние равновесия, где количество жертв равно \( \frac{c}{d} \), поэтому значения \( x_{min}, x_{max} \) выберем на \( \delta% \) меньше и больше стационарного значения соответственно.
Приступим к построению управляемой системы (13) двух популяций.
Для начала, к блок-схеме исходной модели :
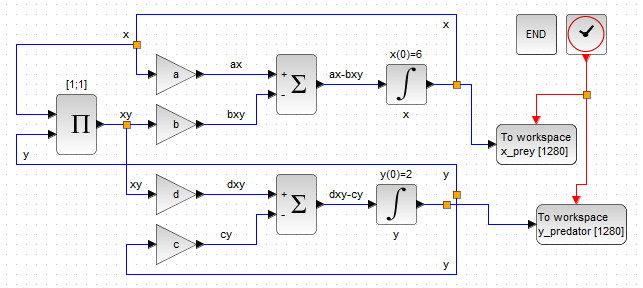
необходимо добавить:
заглушку супер-блока,
блок произведения,
блок TOWS_c.
Следующим шагом нужно провести соединительные линии и отредактировать первый сумматор, как показано на рис. 83.
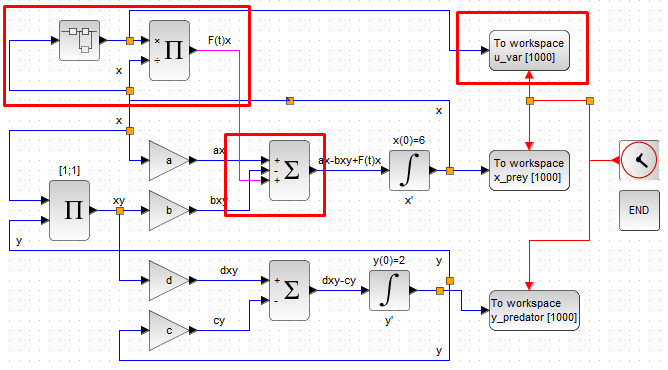
Дальнейшие манипуляции подразумевают задание закона управления (2), за который будет отвечать супер-блок. Щёлкните дважды на супер-блоке, чтобы открыть на редактирование его рабочую область.
Согласно построенной блок-схеме с рис. 83, на вход супер-блока подаётся текущая численность жертв \( x \). Это значение необходимо сравнить со значениями \( x_{min}, x_{max} \) и в зависимости от результата подать на выход супер-блока \( sin(\frac{x}{2}) \) или \( u \), соответственно системе (2).
Сравнение текущего значения численности жертв со значениями \( x_{min}, x_{max} \), инициирующими смену управляющего воздействия, осуществим с помощью блоков индикации смены знака
и 
, которые располагаются на палитре «Обнаружение перехода через нуль» и работают совместно с блоком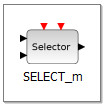 
с палитры «Маршрутизация сигналов», который осуществляет выбор управляющего воздействия.Чтобы воспользоваться блоками NEGTOPOS_f и POSTONEG_f, необходимо привести неравенства из (2) к виду:
(3) \[ \begin{cases} x - x_{min} < 0, &\quad \text{(a)}\\ x - x_{max} > 0, &\quad \text{(b)}\\ \end{cases} \]
Теперь неравенства (3) представляют из себя разность двух элементов, один из которых динамический \( (x) \), а другой – константный, заданный в контексте (значения \( x_{min}, x_{max} \)).
Откуда следует, что для сборки управления, нам дополнительно понадобятся:два константных блока CONST_m
и два сумматора BIGSOM_f.
Предварительное расположение блоков для анализа условий выбора того или иного закона численности жертв, должно выглядеть, примерно, как на рис. 84.
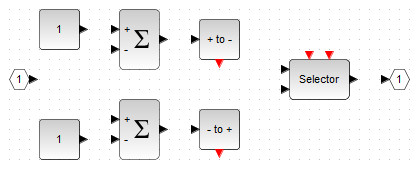
Рассмотрим построение блок-схемы неравенства \( x-x_{min} < 0 \) (3а).
Данное неравенство выполняется, когда значение левой части становится меньше нуля, то есть переходит на тёмную отрицательную сторону оси координат, будучи до это положительным, тем самым осуществляя движения от «+» к «-».
Данному событию соответствует блок, обнаруживающий переход чрез нуль POSTONEG_f. Соответствующая реализация первого неравенства на блок-схеме представлена на рис. 85.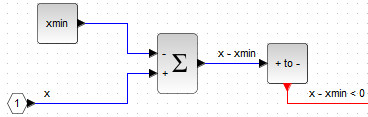
Обратите внимание, что в константном блоке используется значение \( x_{min} < 0 \), которое предварительно задано в контексте и равно \( (1-\delta)\frac{c}{d} \).
Перейдём к неравенству \( x-x_{max} > 0 \) (3b).
Это неравенство выполняется, когда выражение слева превращается из отрицательного в положительное, то есть осуществляется переход через нуль слева направо, за что отвечает блок NEGTOPOS_f.
Реализация данного неравенства полностью повторяет установку соединительных линий предыдущего случая и требует задания значения \( (1+\delta)\frac{c}{d} \) в контексте. Блок схема неравенства (3b) представлена на рис. 86.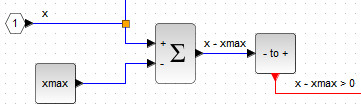
Далее перейдём к реализации выбора нужного закона управления в зависимости от того, какое неравенство из (3) выполняется. Данный выбор осуществляет блок SELECT_m, имеющий два управляющих и два регулярных входа.
На управляющие входы селектора SELECT_m необходимо подать соответствующие красные выходы блоков POSTONEG_f и NEGTOPOS_f. Заметьте, что здесь важен порядок, так как управляющим входам селектора соответствуют его же регулярные входы. Поэтому выход первого неравенства, реализованного блоком POSTONEG_f, нужно соединить с левым управляющим входом селектора, а выход блока NEGTOPOS_f – соединить с правым красным входом блока SELECT_m.До полного сбора блока управления осталось только указать функции управления из системы (2), которые будут использованы при выполнении каждого из условий, поданных на управляющие входы блока SELECT_m.
Для задания управляющих воздействий проделаем следующие действия:на первый регулярный вход селектора подадим функцию \( sin(\frac{x}{2}) \) что соответствует выполнению первого условия (3 а),
а на второй черный вход блока SELECT_m - константу \( u \), заданную в контексте.
Итоговая блок-схема для выбора управляющего воздействия
представлена на рис. 87.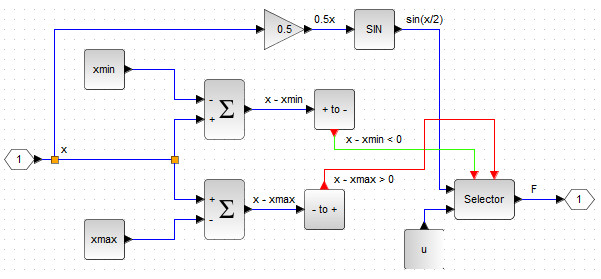
Ниже приведён скрипт, записанный к контексте рабочей области исходной блок-схемы.
Задание контекста в Xcos.clc; a = 1.5; b = 2; d = 0.8; c = 1; delta = 0.03; xmin = (1 - delta)*c/d; xmax = (1 + delta)*c/d; u = -.3; clf(); subplot(211) plot(x_prey.time, x_prey.values, "b", "Linewidth", 2); plot(y_predator.time, y_predator.values, "r", "Linewidth", 2); plot(x_prey.time, 0*x_prey.time + c/d, "black", "Linewidth", 1.2); plot(x_prey.time, 0*x_prey.time + a/b, "magenta", "Linewidth", 1.2); legend("prey","predator", "c/d", "a/b"); xgrid; xtitle("Prey-Predator wth F", "t", "x, y"); subplot(212) plot(u_var.time, u_var.values, "g", "Linewidth", 2); xgrid; xtitle("Control F", "t", "F");
Запустите моделирование на 15сек.. с начальными условиями \( x_0=5, y_0=2 \) соответствующих блоков интеграторов. Результат моделирования представлен на рис. 88.
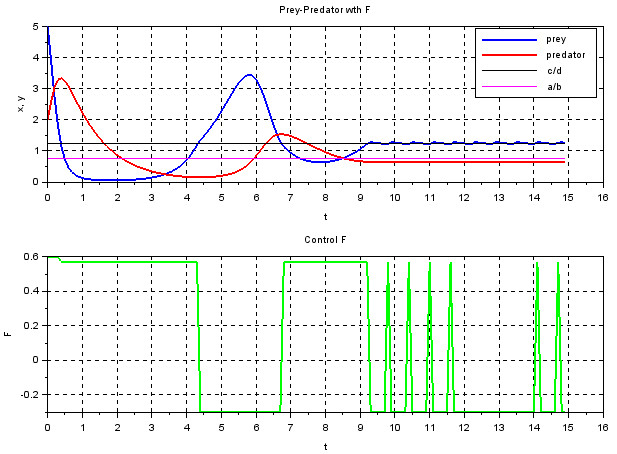
Обратите внимание, что популяция жертв (prey) и хищников (predator) стремится к устойчивым положениям равновесия \( x^* = \frac{c}{d}, y^* = \frac{a}{b} \) соответственно, а отклонения от точек стационарности не превышают заданного значения \( \delta \).
В качестве дополнительного задания и для более подробного изучения динамики системы, читателю предлагается вывести фазовый портрет рассматриваемой системы Хищни-Жертва, убедившись, что траектория сходится к точке устойчивости \( (x^*, y^*) \), а стартует из начальной точки \( (x_0, y_0) \); поменять коэффициенты \( a,b,c,d \) системы в контексте и задать различную степень отклонения \( \delta \), проследив, как меняется взаимодействие популяций.
Комментарии