Использование символьных параметров и контекста в xcos
Приступая к моделированию некоторой динамической системы, часто бывает нужно не раз использовать один и тот же параметр в разных уравнениях или задавать некоторые коэффициенты как функции некоторой переменной величины. Для того, чтобы не создавать одинаковые функциональные блоки, обременяющих схему и для реализации сложных зависимостей, в Xcos предусмотрены символьные параметры и контекст.
Контекст – это код на языке Scilab, который может содержать как простое декларирование переменных, так и создание полноценных самостоятельных Scilab –функций.
Символьные параметры – это непосредственно сами переменные, заданные в контексте, к которым можно обратиться по имени для использования в функциональных блоках при создании блок-схемы.
Рассмотрим использование контекста и символьных параметров на примере создания блок-схемы системы Хищник-Жертва. Данная биологическая система описывает взаимодействие двух видов, один из которых хищники, а второй – жертвы. Изменение популяций во времени описывается системой двух дифференциальных уравнения первой степени вида:
(1)\begin{cases} \dot{x}=ax-bxy\\ \dot{y}=dxy-cy\\ \end{cases}
где \( x \) - популяция жертв. \( y \)- популяция хищников, \( \dot{x}, \dot{y} \)- прирост популяций в момент времени \( t \), \( a \)- темп роста жертв в отсутствии хищников, \( b \) - скорость, с которой хищники поглощают добычу, \( c \) - смертность хищников при отсутствии добычи, \( d\) - скорость, с которой популяция хищников увеличивается, потребляя добычу.
Посмотреть, как можно манипулировать численностью популяций путём ввода управляющего воздействия в данную систему, можно в статье статье.
Создание блок схемы, описывающей взаимодействие двух популяций начнём с задания положительных коэффициентов через контекст.
Для задания контекста кликните правой кнопкой мыши в любом месте рабочей области и выпадающем меню выберите пункт «Установить контекст» (рис. 44 а).
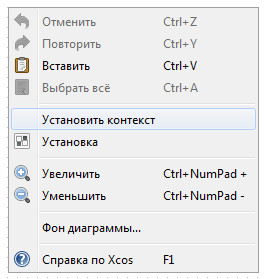
Далее в открывшемся окне задайте значения переменных , как показано на рис. 44 б). После чего нажмите кнопку «ОК».
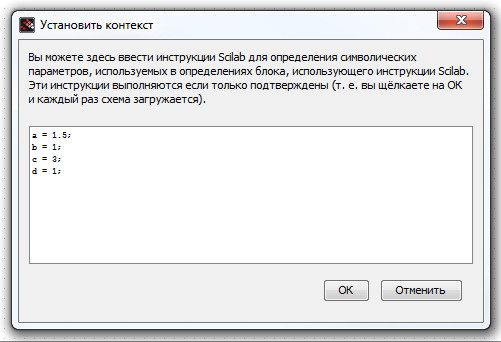
После проделанных манипуляций, вы сможете использовать заданные символьные параметры непосредственно в самих блоках Xcos.
Перечислим блоки, которые будут использованы для создания блок-схемы:
Нам потребуются два блока INTEGRAL_m, так как в системе (1) два уравнения;
Два сумматора, так как и первое, и второе уравнения системы (1) состоят из двух слагаемых;
Для задания множителей нам понадобятся усилители в количестве 4-х штук;
Блоки CLOCK_c и END;
Один блок умножения
 с вкладки «Математические операции» для произведения фазовых переменных;
с вкладки «Математические операции» для произведения фазовых переменных;Два блока
 , располагающихся на палитре «Регистрирующие устройства», с помощью которых будет осуществляться вывод графиков.
, располагающихся на палитре «Регистрирующие устройства», с помощью которых будет осуществляться вывод графиков.
Итак, приступим.
Создадим заготовку для каждого из уравнений (1), представляющих собой интеграл от суммы, при этом, укажем начальную численность хищников и жертв в 2 и 6 особей соответственно, как показано на рис. 45.
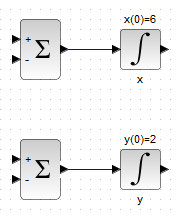
Далее создадим первое слагаемое \( ax \) из первого уравнения, как усиленное в \( a \) раз произведение результата интегрирования (см. рис. 46) . Обратите внимание, что в блок GAINBLK в данном случае имеет значение символьного параметра \( a \).
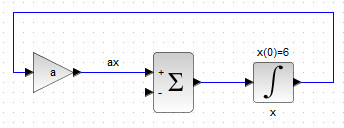
Второе слагаемого первого уравнения \( \dot{x}=ax-bxy \) представляет собой произведение переменных \( x,y \), образующихся на выходах блоков INTEGRAL_m, которое усиливается в \( b \) раз и подаётся на вход блока BIGSOM_f со знаком «-», как показано на рис. 47.
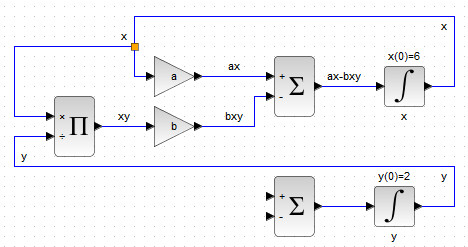
По аналогии с пунктами 2-3 необходимо провести соединительные линии, обеспечивающие связи блоков для создания уравнения хищников \( \dot{y}=dxy-cy \), входящего в систему (1). Обратите внимание, что во втором уравнении фигурирует множитель \( xy \) с коэффициентом усиления \( d \). Данный множитель присутствует и в уравнении для жертв и формируется на выходе блока-произведения, поэтому дублирование данного произведения излишне, потребуется лишь распараллелить выход блока. В результате должна получиться блок-схема, показанная на рис. 48.
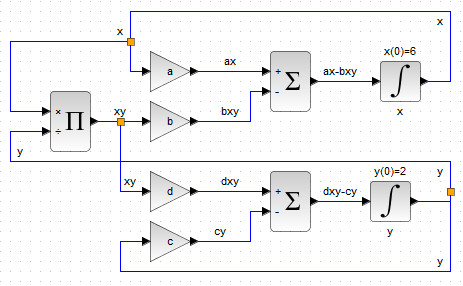
Далее подсоедините регулярные выходы интегральных блоков INTEGRAL_m ко входам TOWS_c, а управляющие входы блоков TOWS_c – параллельно соедините со входом блока CLOCK_C (см. рис. 49).
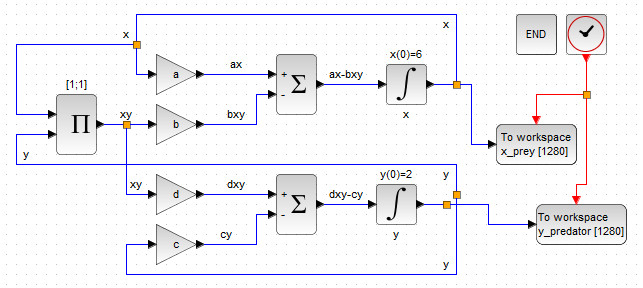
Блок TOWS_c собирает в буфер данные моделирования для дальнейшего их использования в контексте. У данного блока нам интересны следующие внутренние параметры: Size of buffer - размер входного буфера, это общее количество значений входной переменной, записанных во время моделирования; Scilab variable name - имя переменной Scilab, по которому в последующем в контексте можно будет обратиться к значениям, записанным в конкретном буфере.
Для буфера, принимающего на вход переменную задайте Scilab variable name=x_prey. Для буфера, принимающего на вход переменную задайте Scilab variable name=y_predator. Размер буфера в обоих случаях установите равным 1280.
Запустите моделирование на 10 сек. и убедитесь, что не возникает ошибок моделирования. Но и графики не появляются.
Для того, чтобы увидеть графическую и интерпретацию колебаний численности популяций, прибегнем к использованию в контексте заданных переменных x_prey и y_predator.
Откройте окно добавления контекста и добавьте к уже имеющимся строкам следующие:
Задание контекста в Xcos.plot(x_prey.time, x_prey.values, "b", "Linewidth", 2); plot(y_predator.time, y_predator.values, "r", "Linewidth", 2); legend("Жертвы","Хищники"); xgrid; xtitle("Модель Хищник-Жертва", "t, время", "x, y");После запуска моделирования появится окно с одной системой координат с заголовком, подписанными осями и двумя графиками, как показано на рис. 50.
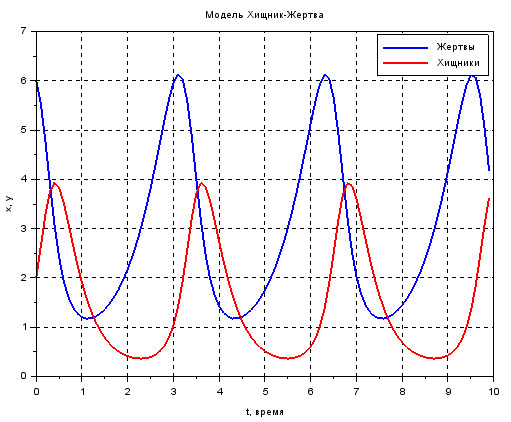
Обратите внимание, что численность популяций (2-е хищников и 6 жертв) в нулевой момент времени соответствует начальным условиям, заданным в параметрах блоков – интеграторов.
Анализируя график численности популяций, можно сделать следующие выводы:
численность хищников всегда отстаёт от популяции жертв;
когда популяция жертв высока, хищники начинают быстро размножаться из-за обилия пищи;
когда хищников становится слишком много, популяция жертв начинает стремительно сокращаться;
при недостаточной численности жертв, поголовье хищников начинает сокращаться из-за недостатка пищи;
когда популяция хищников мала, популяция жертв увеличивается из-за низкого уровня смертности.
Итак, на примере создания блок-схемы математической модели взаимодействия двух популяций, мы рассмотрели возможность задания переменных в контексте Xcos и их последующего использования в функциональных блоках. Кроме того, мы научились пользоваться блоками буферизации TOWS_c и познакомились порядком использования встроенных функций Scilab для построения и настройки отображения графиков.
Посмотреть, как можно манипулировать численностью популяций путём ввода управляющего воздействия в данную систему, можно в статье статье.

Комментарии