Матричные уравнения в Scilab Xcos
Ранее были рассмотрены несколько подходов к визуальному моделированию динамических систем, а именно:
В данном материале будет рассмотрен подход к построению блок-схемы динамических систем, которые описываются матричными уравнениями. В связи с тем, что Scilab разрабатывается, как матрично-ориентированное программное обеспечение, представление динамических систем именно в матричном, а не покоординатном виде – есть наиболее оптимальный способ решения поставленных задач, потому что сам инструмент под это заточен, да и использование матриц и векторов позволяет избежать некоторых ошибок, которые бы имели место быть при их реализации с использованием других подходов.
Немного теории
В современной теории управления далеко не редкость - представление динамических систем в виде пространства состояний, так как это позволяет избежать ограничений, накладываемых на передаточные функции, использование которых присуще классическому подходу для решения задач управления.
Модель системы, построенная в пространстве состояний предполагает использование ОДУ первого порядка. Если же для описания процесса функционирования рассматриваемой системы требуется использование дифференциальных уравнений порядка выше 1, каждое из таких уравнений сводится в совокупности ОДУ первого порядка, что всегда возможно, как было сделлано с помощью пользовательских функций Scilab и блоков Xcos.
При этом, переменные, которые используются для составления дифференциальных уравнений, называются фазовыми координатами и полностью описывают динамическую систему и её реакцию на определённые входные данные. Число фазовых переменных равняется порядку ОДУ, описывающему динамическую систему. Кроме того, фазовые переменные – это как раз те переменные, для которых задаются начальные условия, число которых, как известно, также, совпадает со степенью исходного ОДУ.
Модель пространства состояний формируется из уравнений входа и выхода, где для случая управляемой линейной системы из \(n\) переменных состояния, имеющей \(p\) входов и \(q\) выходов, матричные уравнения имеют вид:
(1) \[ \begin{cases} \dot x(t) = A(t)x(t)+B(t)u(t)\\ \dot y(t) = C(t)x(t)+D(t)u(t)\\ \end{cases} \quad\quad\text{где} \quad x(t)\in \mathbb{R}^n, y(t)\in \mathbb{R}^q, u(t)\in \mathbb{R}^p \]
\(x=(x_1,x_2,...,x_n)^T \) - вектор состояния, элементы которого называются состояниями системы,
\(y=(y_1,y_2,...,y_q)^T \)- вектор выхода,
\(u=(u_1,u_2,...,u_p)^T \)- вектор управления,
\( A_{n\times n} \)- матрица системы,
\( B_{n\times p} \)- матрица управления,
\( C_{n\times q} \)- матрица выхода,
\( D_{q\times p} \)- матрица прямой связи.
Структурная схема описанной системы представлена на рис. 89.
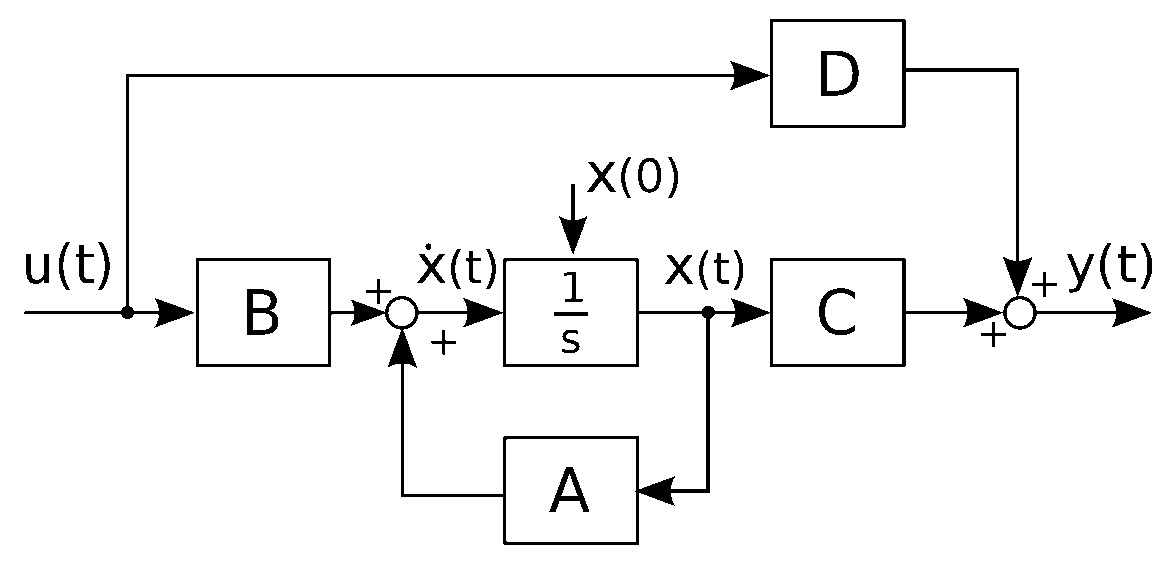
Управление грузом на пружине с демпфером
Разобравшись с терминологией, перейдём к примерам. Рассмотрим груз массы \(m\) с закреплённой пружиной жёсткости \(k\) и демпфером с коэффициентом демпфирования \(c\), движение которого осуществляется при помощи силы \(F\) (см. рис. 90)
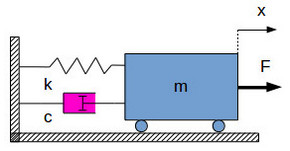
Уравнения движения описанного груза имеют вид:
(2) \[ F-kx-c\frac{dx}{dt}-m\frac{d^2x}{dt^2}=0 \]
В принципе, уравнения (2) уже достаточно, чтобы собрать его блок-схему с использованием подходов, рассмотренных ранее. Однако наша цель – матрицы, которые на данном этапе не видны.
Прежде всего, определим, степень рассматриваемого уравнения. Наибольшая производная, фигурирующая в (2) – второго порядка, стало быть, перед нами ОДУ 2-го порядка.
В статье рассматривался способ решения подобного дифференциального уравнения, путём сведения его к системе. Этот подход и лежит в основе представления динамической системы в пространстве состояний. Вспомним, что мы делали:
1) переписывали уравнения так, чтобы слева от знака равно осталась наивысшая производная,
2) делали замену и получали систему.
Приступим. Преобразуем (2) к желаемому виду:
(3) \[ \ddot{x}=\frac{1}{m}\left( -c\dot x-kx+F \right) \]
Вопрос, сколько получится ОДУ первой степени из ОДУ 2-й степени? Правильно, два. Вторая степень уравнения, - два уравнения в системе. А как получить эти два уравнения? Правильно, ввести переменные состояния . Вторая степень уравнения – две переменных состояния. Введём замену:
(4)\[ \begin{cases} z_1 = x\\ z_2 = \dot x\\ \end{cases} \quad\quad \Rightarrow \begin{cases} \dot z_1 = \dot x\\ \dot z_2 = \ddot x\\ \end{cases} \]
Итак, исходно обыкновенное дифференциальное уравнение второй степени (2), путём замены (4) сводится к системе из двух ОДУ первой степени:
(5)\[ \begin{cases} \dot z_1 = z_2\\ \dot z_2 = \frac{1}{m}\left( -cz_2-kz_1+F \right) \\ \end{cases} \]
На первый раз, раскроем скобки в (5) и запишем фазовые переменные друг под другом:
\[ \begin{cases} \dot z_1 = \quad 0\cdot z_1 + \;\;\;1\cdot z_2 + 0\cdot F\\ \dot z_2 = -\frac{k}{m}\cdot z_1 -\frac{c}{m}\cdot z_2 + \frac{1}{m}\cdot F \\ \end{cases} \]
Запишем систему (5) в матричной форме:
(6) \[ \begin{pmatrix} \dot z_1 \\ \dot z_2 \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ -\frac{k}{m} & -\frac{c}{m} \end{pmatrix} \begin{pmatrix} z_1 \\ z_2 \end{pmatrix} + \begin{pmatrix} 0 \\ \frac{1}{m} \end{pmatrix} F \]
Теперь, мы с лёгкостью можем определить матрицу состояний:
\[ A_{2\times 2}= \begin{pmatrix} 0 & 1 \\ -\frac{k}{m} & -\frac{c}{m} \end{pmatrix} \]
и матрицу управления:
\[ B_{2\times 1}= \begin{pmatrix} 0 \\ \frac{1}{m} \end{pmatrix} \]
Для определения выходного вектора \( y \) и матриц \( C,D \) , нужно обозначить величину, измеряемую на выходе. Допустим, мы хотим измерять положение груза, следовательно, выходное уравнение будет иметь вид:
\( y=z_1 \)
соответственно, в матричной форме:
\[ \begin{pmatrix} y_1 \\ y_2 \end{pmatrix} = \underbrace{ \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix} }_\text{C} \begin{pmatrix} z_1 \\ z_2 \end{pmatrix} + \underbrace{ \begin{pmatrix} 0 \\ 0 \end{pmatrix} }_\text{D} F \]
В итоге, получим следующую динамическую модель движущегося груза в пространстве состояний:
(7) \[ \begin{cases} \dot z = \begin{pmatrix} 0 & 1 \\ -\frac{k}{m} & -\frac{c}{m} \end{pmatrix} z + \begin{pmatrix} 0 \\ \frac{1}{m} \end{pmatrix} F \\ y= \begin{pmatrix} 1 & 0 \end{pmatrix} z \end{cases} \]
Последний штрих, перед тем, как перейти к визуальному моделированию указать начальные условия для системы (7). Напомним, число н.у.=числу переменных состояния=порядку исходного ДУ. Мы рассматриваем уравнение второго порядка, следовательно, необходимо задать два начальных условия для каждой из фазовых переменных: \( z_{1}^{0}=0, z_{2}^{0}=0 \)
Перейдём к построению блок-схемы тележки с демпфером в Xcos
Для задания динамической системы в формате (7) используется блок
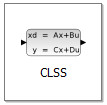 с вкладки «Системы с непрерывным временем». Во внутренних параметрах данного блока нужно в Scilab- формате задания матриц и векторов, записать соответствующие матрицы. Мы не будем прибегать к непосредственной записи матриц в блоке, а зададим их в контексте, чтобы в дальнейшем в параметрах блока CLSS использовать только соответствующие переменные.
с вкладки «Системы с непрерывным временем». Во внутренних параметрах данного блока нужно в Scilab- формате задания матриц и векторов, записать соответствующие матрицы. Мы не будем прибегать к непосредственной записи матриц в блоке, а зададим их в контексте, чтобы в дальнейшем в параметрах блока CLSS использовать только соответствующие переменные.Откройте на редактирование контекст рабочей области и задайте матрицы и вектора, используемые в системе (7), особое внимание стоит уделить форме задания строки \(C\):
Векторно-матричные элементы системы (7) в контексте XcosA = [0 1; -k/m -c/m]; B = [0; 1/m]; C = [1; 0]'; D = 0;Далее в контексте необходимо задать начальные условия \( z_{1}^{0}=0, z_{2}^{0}=0 \) в виде вектор-строки:
Задание начальных условий в контексте XcosZ0 = [0 0];И указать параметры системы:
Задаём переменные в контексте Xcosm = 2; c = 1; k = 2;После чего, необходимо сохранить контекст и заполнить поля внутренних параметрах блока CLSS , как показано на рис. 91.
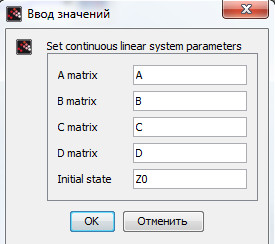
Для дальнейшего построения блок-схемы потребуются 4 блока: CLOCK_c, END, CSCOPE и блок
 , который находится на палитре «Источники сигналов и воздействий». Блоки необходимо связать между собой соединительными линиями, как показано на рис. 92, настроить параметры осциллографа и запустить моделирование на 22с.
, который находится на палитре «Источники сигналов и воздействий». Блоки необходимо связать между собой соединительными линиями, как показано на рис. 92, настроить параметры осциллографа и запустить моделирование на 22с. 
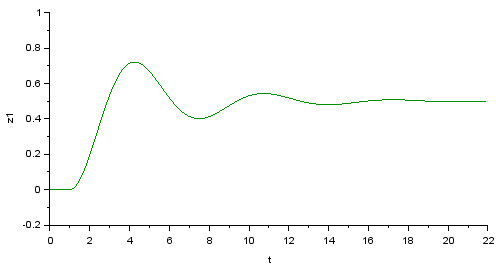
В результате моделирования на экране появится график затухающих синусоидальных колебаний, соответствующий переменной \(z_1\), то есть, координате передвигаемого груза (рис. 93).
Блок STEP_FUNCTION функционирует согласно правилу:
\[ step_f(t)= \begin{cases} s_0, \quad t < t_0 \\ s_f, \quad t > t_0 \\ \end{cases} \]
где \(t_0, s_0,s_f\) - параметры, которые задаются во внутренних параметрах блока STEP_FUNCTION следующим образом:
\(t_0\)- это параметр Start Time,
\(s_0\)- это параметр Initial Value,
\(s_f\)- это параметр Final Value.
В нашем случае, параметры у блока STEP_FUNCTION остались выставленные по умолчанию, поэтому, он на протяжении 1сек. подаёт на выход значение «0», а в последующие моменты времени – значение «1», что прослеживается на графике (рис. 93).
Выводим график скорости груза
После запуска моделирования возникает справедливый вопрос, а почему переменная только одна и как же вывести фазовый портрет системы?
Прежде всего, отметим, что на выход блока CLSS подаётся переменная \(y\), которая формируется, как выход системы (7). Обратимся к системе (7) и её уравнению выхода
\[ \begin{pmatrix} y_1 \\ y_2 \end{pmatrix} = \underbrace{ \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix} }_\text{C} \begin{pmatrix} z_1 \\ z_2 \end{pmatrix} \]
где не обнуляется только фазовая переменная \(z_1\), соответствующая переменной выхода с координатой \(y_1\) . Становится понятно, что, собственно, хотели получить на выходе \(y\) - то и получили – переменную состояния \(z_1\), которая отвечает за положение груза \(x\). Но мы сами настроили выход таким образом, а значит, его можно изменить.
Если бы нам потребовалось, например, построить график скорости груза, а скорость, -это, как известно – \(\dot x\) , то и в уравнении выхода нужно было бы обращаться к фазовой переменной \(z_2\), отвечающей за скорость. Следовательно, уравнение выхода в системе (7) для случая вывода скорости грузу, преобразуется к виду
\[ \begin{pmatrix} y_1 \\ y_2 \end{pmatrix} = \underbrace{ \begin{pmatrix} 0 & 0 \\ 0 & 1 \end{pmatrix} }_\text{C} \begin{pmatrix} z_1 \\ z_2 \end{pmatrix} \]
или сокращённо:
\[ y=\begin{pmatrix} 0 & 1 \end{pmatrix}z \]
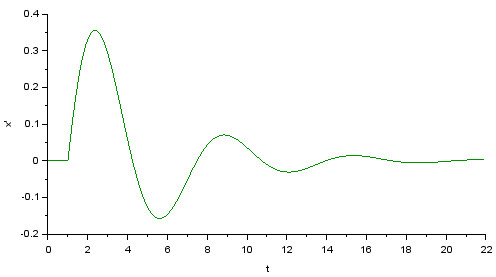
Отредактировав вектор в контексте, запустите моделирование, результатом которого будет график, изображённый на рис. 94.
Строим траектории фазовых переменных системы в Xcos
Рассмотрим теперь задачу вывода нескольких переменных состояния и построения траектории на фазовой плоскости.
Обратимся к ранее составленным уравнениям выхода. В первом случае матричное уравнение
\[ \begin{pmatrix} y_1 \\ y_2 \end{pmatrix} = \underbrace{ \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix} }_\text{C} \begin{pmatrix} z_1 \\ z_2 \end{pmatrix} \]
подаёт на выход \( y_1 \) фазовую переменную \( z_1 \), потому что только элемент \( c_{11} \) матрицы выхода \( C \) не обнуляется.
Соответственно для вывода фазовой переменной \( z_2 \) справедливо уравнение
\[ \begin{pmatrix} y_1 \\ y_2 \end{pmatrix} = \underbrace{ \begin{pmatrix} 0 & 0 \\ 0 & 1 \end{pmatrix} }_\text{C} \begin{pmatrix} z_1 \\ z_2 \end{pmatrix} \]
где ненулевым оказывается элемент \( c_{22} \)
Теперь, если обобщить полученную информацию, можно сделать вывод, что для вывода переменной состояния \( z_k \), в матрице выхода должна стоять «1» на месте \( c_{kk} \). Соответственно, для передачи на выход обеих переменных состояния рассматриваемой двумерной системы (7), матрица \( C \) преобразуется в единичную матрицу размера 2х2, при этом, размерность вектора \( y \) становится равной количеству выводимых переменных, т.е. «2».
Таким образом, линейная динамическая система в пространстве состояний, описывающая движение груза с пружиной и демпфером, подающая на выход обе фазовых переменных, примет вид:
(8) \[ \begin{cases} \dot z = \begin{pmatrix} 0 & 1 \\ -\frac{k}{m} & -\frac{c}{m} \end{pmatrix} z + \begin{pmatrix} 0 \\ \frac{1}{m} \end{pmatrix} F \\ y= \begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix} z \end{cases} \]
Для моделирования системы (8), прежде всего, в контексте нужно изменить строку, где задаётся матрица выхода:
C = eye(2,2);
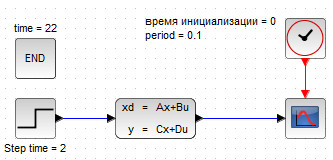
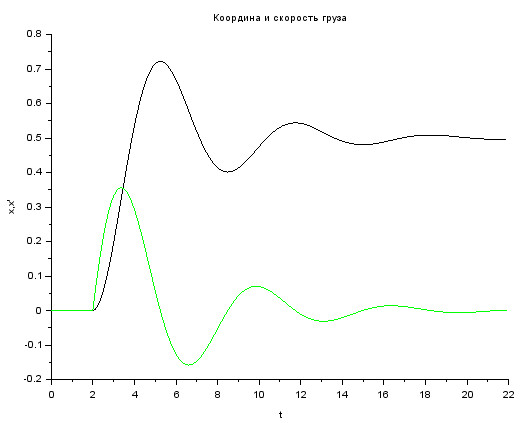
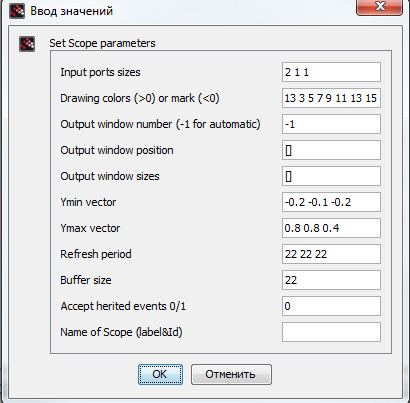
После чего необходимо заменить одномерный осциллограф на блок CMSCOPE, размерность входа которого нужно исправить на 2. На рис.95а) приведена блок-схема с векторным осциллографом, а на рис. 95 б) – результат моделирования системы (8).
Строим графики динамической системы на разных координатных сетках в Xcos
А что, если в ходе моделирования потребуется построить графики переменных состояния на отдельных системах координат?
В этом случае потребуется воспользоваться блоком  , который располагается на палитре «Маршрутизация сигналов». Данный
блок разделяет входной поток на отдельные составляющие. В нашем случае на вход блока DEMUX попадает вектор \( y \) условной размерности 2, который на выходе превращается в отдельные вектора фазовых выходных переменных \( y_1 \) и \( y_2 \). Использования блока расщепления DEMUX представлено на рис. 96.
, который располагается на палитре «Маршрутизация сигналов». Данный
блок разделяет входной поток на отдельные составляющие. В нашем случае на вход блока DEMUX попадает вектор \( y \) условной размерности 2, который на выходе превращается в отдельные вектора фазовых выходных переменных \( y_1 \) и \( y_2 \). Использования блока расщепления DEMUX представлено на рис. 96.
Результат моделирования и внутренние параметры блока CMSCOPE представлены на рис. 97а-б).
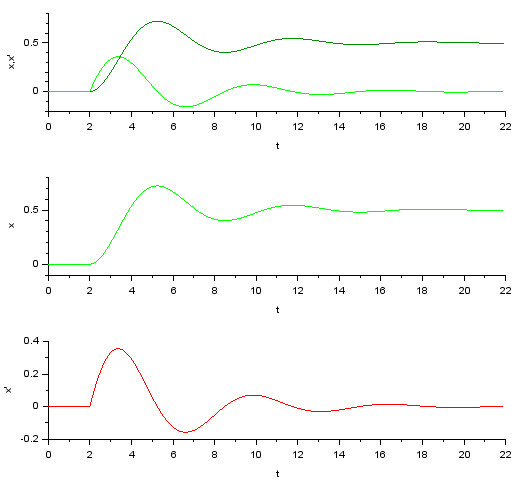
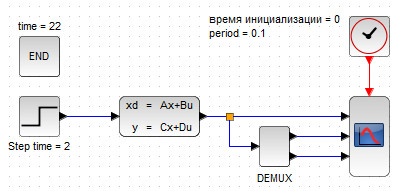
Продолжим модернизировать созданную блок-схему и на следующем шаге откажемся от осциллографа, заменив его блоком TOW_c. Использование блока записи в контекст предпочтительнее, так как последний предоставляет больше возможностей для редактирования и отображения графической информации посредством использования контекста.
Блоки многомерного осциллографа CMSCOPE и расщепления можно удалить – они не понадобятся.
Блок-схема системы с внесёнными изменениями показана на рис. 98.

Напомним, что на вход блока TOW_c подаётся вектор, который в переменную y_var, а потом используется в контексте для построения графиков. Чтобы понять, что за объект формируется в переменной y_var, его можно вывести в консоль с помощью стандартной функции Scilab disp().
Добавьте в контекст строку очистки консоли и вывода переменной:
clc;
disp(y_var);
Запустите моделирование и перейдите в консоль. В командном окне Scilab Вы обнаружите следующее:

Итак, рисунок 99 гласит о том, что объект y_var содержит два атрибута: вектор \( values \), в котором 2 столбца и 220 строк и вектор \( time \) – временные отсчёты, представляющие собой вектор-столбец с 220 значениями.
Если подробнее, то вектор y_var\(.time\) – это точки в которых вычисляются значения системы, их 220 потому, что моделирование происходит на протяжении 22сек. со значением \( period=0.1 \). Вектор y_var\(.values\) в первом столбце содержит значения первой фазовой переменной \( z_1 \), поданной на выход системы, т.е. значения координаты \( x \), вычисленные в каждой из 220 моментов времени; а во втором столбце – значения второй фазовой переменной \( z_2 \), которая соответствует производной \( \dot{x} \), то есть скорости груза, вычисленные в тех же 220 точках.
Для построения покоординатных графиков и фазового портрета нам предстоит обращаться к значениям y_var\(.values\) содержащимся в первом и втором столбцах по-отдельности.
Например, для того, чтобы получить все значения первого столбца, соответствующие переменной состояния \(z_1\), необходимо записать: y_var . values(: , 1), соответственно, чтобы получить значения вектора скорости, нужно использовать запись y_var . values(: , 2).
С помощью скрипта, записанного в контексте, можно получить одно графическое окно с 4-мя системами координат, как на рис. 100
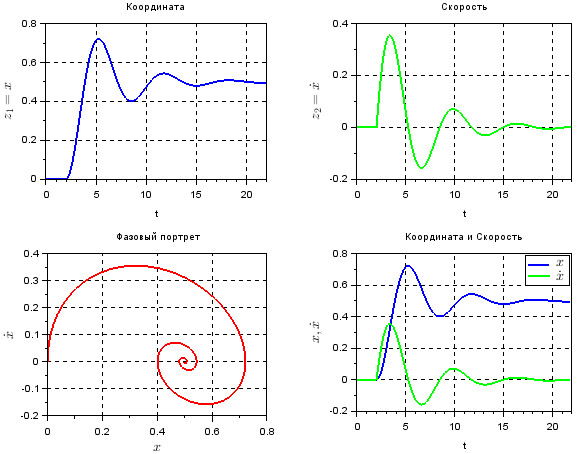
Контекст, реализующий задание матриц системы, представленной в пространстве состояний и строящий графики следующий:
clc;
clc;
m = 2; c = 1; k = 2;
A = [0 1; -k/m -c/m];
B = [0; 1/m];
C = eye(2,2);
D = 0;
Z0 = [0 0];
clf();
subplot(221)
plot(y_var.time, y_var.values(:,1), "b", "Linewidth", 2);
xgrid;
xtitle("Координата", "t", "$\Large z_1 = x$");
subplot(222)
plot(y_var.time, y_var.values(:,2), "g", "Linewidth", 2);
xgrid;
xtitle("Скорость", "t", "$\Large z_2=\dot{x}$");
subplot(223)
plot(y_var.values(:,1), y_var.values(:,2), "r", "Linewidth", 2);
xgrid;
xtitle("Фазовый портрет", "$\Large x$", "$\Large \dot{x}$");
subplot(224)
plot(y_var.time, y_var.values(:,1), "b", "Linewidth", 2);
plot(y_var.time, y_var.values(:,2), "g", "Linewidth", 2);
legend("$\Large x$","$\Large \dot{x}$"); xgrid;
xtitle("Координата и Скорость", "t", "$\Large x,\dot{x}$");

Комментарии