Анимация стабилизации маятника в Scilab
На примере простой механической системы посмотрим, как "оживить" картинки в Scilab без дополнительных плагинов и без использования comet().
Будем стабилизировать простой математический маятник.
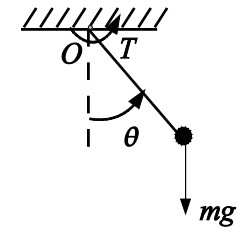
Уравнения которого имеют вид.
\( \ddot{\theta} + b\dot{\theta} + asin\theta = cT \)
Стабилизировать маятник будем в программной позиции \( \theta = \delta=const \) с помощью вращающего момента: \( T = u \)
\( \ddot{\theta} + b\dot{\theta} + asin\theta = cu \) (1)
Найдём программное управление \( u^p \)
Программное управление \( u^p \) - это управление, которое обеспечивает программную позицию, т.е. отклоняет маятник на угол \( \delta \). Подставим \( \theta = \delta \) в (1):
\( \ddot{\delta} + b\dot{\delta} + asin\delta = cu^p \)
Так как угол \( \delta \) - это постояннная величина, ведь мы хотим, чтобы маятник остановился в таком положении, её производные будут равны 0, следовательно:
\( 0 + 0 + asin\delta = cu^p \)
Откуда можно выразить искомое программное управление \( u^p \):
\( u^p = \frac{a}{c}sin\delta\) (2)
Перейдём к системе д.у.
Подробно переход к системе ДУ рассматривается в этом материале.
Введём фазовые координаты:
\( x_1 = \theta, x_2 = \dot{\theta} \)
Тогда исходное уравнение (1) второго порядка сведётся к системе из двух дифференциальных уравнений первого порядка:
\begin{cases} \dot{x_1} = x_2 \\ \dot{x_2} = cu - bx_2 - asinx_1 \quad (3)\end{cases}
Программная позиция для системы
Наша задача - обеспечить скорейшую остановку маятника в заданной позиции, т.е. перевести маятник в позицию \( \theta = \delta \), где скорость=0. Запишем это условие для фазовых координат
\( x_1 = \delta, x_2 = \dot{\delta} = 0 \)
Итак, для системы (3) нас интересует позиция:
\begin{cases} \dot{x_1} = \delta \\ \dot{x_2} = 0 \quad (4) \end{cases}
Для того, чтобы к системе (3) можно было применят теоремы об асимтотической устойчивости нулевого положения равновесия, нам неоходимо перенести систему коордиинат в точку, где позиция \( (\delta, 0) \) - это нуль.
Переход к системе в отклонениях
Введём отклонения от программной позиции (4) в системе (3):
\begin{cases} y_1 = x_1 - \delta \\ y_2 =x_2 - 0 \end{cases} (5) \begin{cases} x_1 = y_1 + \delta \\ x_2 =y_2 \end{cases}
Подставим (5) в (3), тогда система в отклонениях примет вид:
\begin{cases} \dot{y_1} = y_2 \\ \dot{y_2} = cu - by_2 - asin\left( y_1 + \delta \right) \end{cases}
Корректировка управляющего воздействия
Как правило, для эффективного управления динамическими системами одного программного управления \( u^p \) бывает недостаточно из-за неточностей в измерениях и влияния внешних источников, поэтому мы введём добавочное стабилизирующее управление \( u^{st}\) :
\( u = u^p + u^{st} \)
Тогда системе в отклонениях получим:
\begin{cases} \dot{y_1} = y_2 \\ \dot{y_2} = c\left( u^p + u^{st} \right) - by_2 - asin\left( y_1 + \delta \right) \end{cases}, или \begin{cases} \dot{y_1} = y_2 \\ \dot{y_2} = c \cdot \frac{a}{c} sin\delta\ + c \cdot u^{st} - by_2 - asin\left( y_1 + \delta \right) \end{cases}, что приводит к \begin{cases} \dot{y_1} = y_2 \\ \dot{y_2} = asin\delta\ + cu^{st} - by_2 - asin\left( y_1 + \delta \right) \quad (6) \end{cases}
Линеаризация системы в отклонениях
Так как эффективнее всего теоремы об устойчивости работают для линейных систем, начнём с линеаризации системы (6).
Разложжим \( sin\left( y_1 + \delta \right) \) в окрестности нуля:
\( sin\left( y_1 + \delta \right) \sim y_1cos(\delta) + sin\delta \)
Подставляя данное разложение в (6), получим:
\begin{cases} \dot{y_1} = y_2 \\ \dot{y_2} = asin\delta\ + cu^{st} - by_2 - ay_1cos(\delta) - asin\delta \end{cases}
Таким образом, система (6) примет вид:
\begin{cases} \dot{y_1} = y_2 \\ \dot{y_2} = - acos(\delta)y_1 - by_2 + cu^{st} \quad (7) \end{cases}
Запишем систему (7) в векторно-матричном виде, чтобы с ней было бы удобнее работать:
\begin{matrix} \dot y= { \begin{pmatrix} 0 & 1 \\ - acos(\delta) & -b \end{pmatrix} } y + { \begin{pmatrix} 0 \\ c \end{pmatrix} } u^{st} \quad (8) \end{matrix}
Найдём стабилизирующее управление \(u^{st} \)
Прежде всего, сделаем из системы (8) однородную систему. Для этого выберем \(u^{st} \) вида:
\( u^{st}= -Ky, \quad K = (k_1, k_2) \quad (9) \)
и подставив (9) в (8), получим чудесную линейную однородную систему дифуров:
\begin{matrix} \dot y= { \begin{pmatrix} 0 & 1 \\ - acos(\delta)-сk_1 & -b-ck_2 \end{pmatrix} } y \quad (10) \end{matrix}
Стабилизиирующее управление \(u^{st} \) - это управление, которое стабилизирует систему. То есть обеспечивает асимтотическую устойчивость нулевого положения равновесия этой системы.
В обычных условиях, система (10) сосвем не обязательно будет ас. устойчивой, но чтобы победить эту несправедливость мы и ввели управление \(u^{st} \) в виде \( u^{st}= -Ky \), подрегулировав значения \(k_j \) которого, мы добьёмся того, чтобы корни характеристического уравнения системы (10) были бы "левыми".
Значения \(k_j \), кстати, называются коэфффицентами усиления.
Итак, нам предстоит найти условия на основе \(k_j \), при которых собственные значения матрицы
\begin{matrix} { \begin{pmatrix} 0 & 1 \\ - acos(\delta)-сk_1 & -b-ck_2 \end{pmatrix} } \quad (11) \end{matrix}
были бы расположены в левой полуплоскости комплекной плоскости.
Условия гурвицевости матрицы (11)
Чтобы не утруждаться поиском с.з. и с.в. матрицы (11), воспользуемся критерием асисмтотической устойчивости вида:
\begin{cases} trA < 0 \\ |A| > 0 \end{cases}
Откуда получим условия на \(k_1 \) и \(k_2 \) :
\begin{cases} k_2 > -\frac{b}{c} < 0 \\ k_1 > \frac{a}{c}cos(\delta) \end{cases}
Итак, выбирая стабилизирующее упарвление в виде:
\(u^{st} = -k_1y_1 - k_2y_2 \)
мы добьёмся стабилизации линейной системы в отклонениях (7), что, в свою очередь будет значить схождение моделируемого движения маятника к программной позиции при решении задачи стабилизации положения равновесия, где управление будет складываться из программного и стабилизирующего управлений
\(u = u^p + u^{st} \)
Программная реализация
Приступим, наконец, к моделированию процесса стабилизации математического маятника в Scilab. Для этого нам понадобятся:
- Система (3)
- Управление (2)
- Управление (12)
- Замена (5)
Сначала зададим параметры, фигурирующие в системе:
g = 9.8;
m = 2;
k = 0.9;
L = 3.5;
b = k/m;
a = g/L;
c = 1/(m*L*L);
Далее зададим программное положение \(\delta \) и пaраметры стабилизирующего управления \(k_j \):
delta = %pi/5;
k1 = .1;
k2 = 10;
Зададим начальные условия, шаг дискретизации и отрезок интегрирования для решения системы ОДУ в Scilab:
Xo = [2.1; 0.5]; // Здесь первые два элемента - это н.у. (координата и скорость)
tmax = 20;
t0 = 0;
t = 0:1e-2:tmax;
X = ode(Xo, t0, t, systNelin);
И, наконец, запишем функцию, которая отвечает за формирование системы дифуров, описывающих движение маятника с найденным управлением:
function dx = systNelin(t, x)
y(1) = x(1) + delta;
y(2) = x(2);
Up = a/c * sin(delta);
Ust = -k1*y(1) - k2*y(2);
U = Up + Ust;
dx(1) = x(2);
dx(2) = c*U - b*x(2) - a*sin(x(1));
endfunction
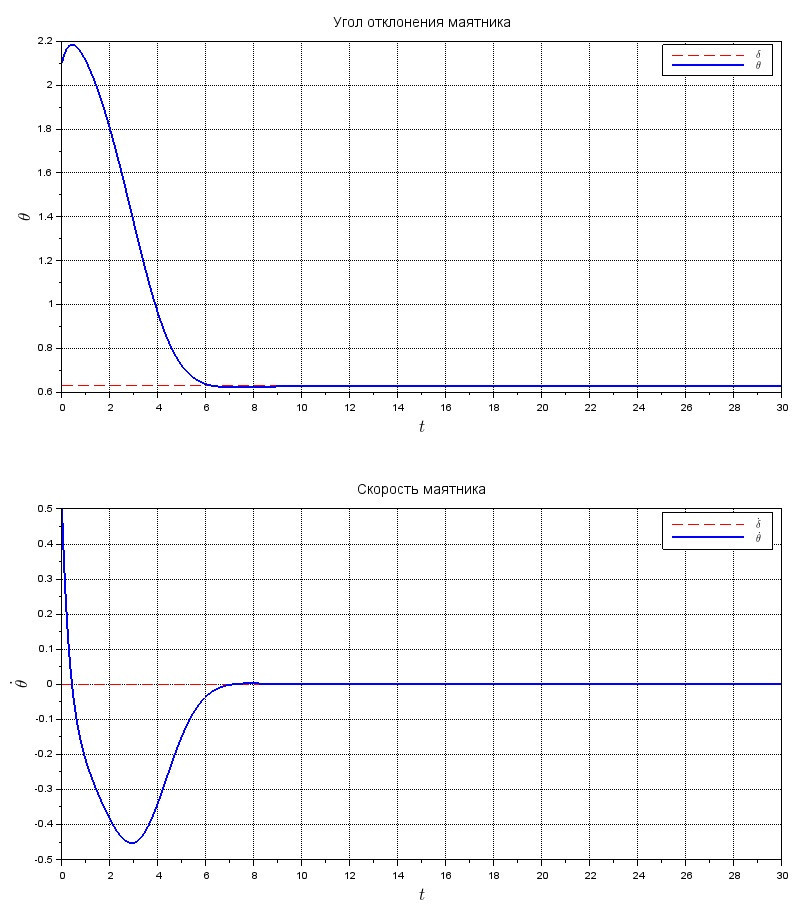
Этого, в принципе, достаточно, чтобы получить статическую графическую интерпретацию решения нашей задачи.
subplot(121);
xgrid();xtitle("Угол отклонения маятника", "$\Large t$", "$\Large \theta$");
plot(t, t*0 + delta,'r--');
plot(t, X(1,:),'b');
gca().children.children(1).thickness = 2;
legend('$\delta$','$\theta$');
subplot(122);
xgrid();xtitle("Скорость маятника", "$\Large t$", "$\Large \dot\theta$");
plot(t, t*0 + 0,'r--');
plot(t, X(2,:),'b');
gca().children.children(1).thickness = 2;
legend('$\dot\delta$','$\dot\theta$');
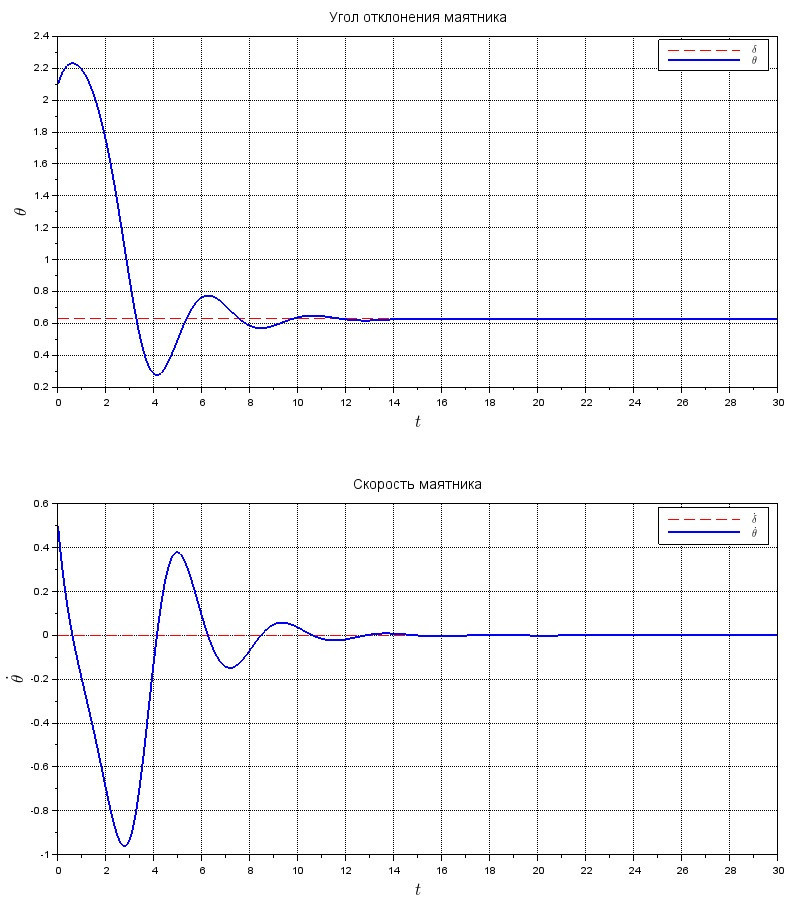
При этом, подправляя коэффициеты усиления, можно регулировать скорость сходимости.
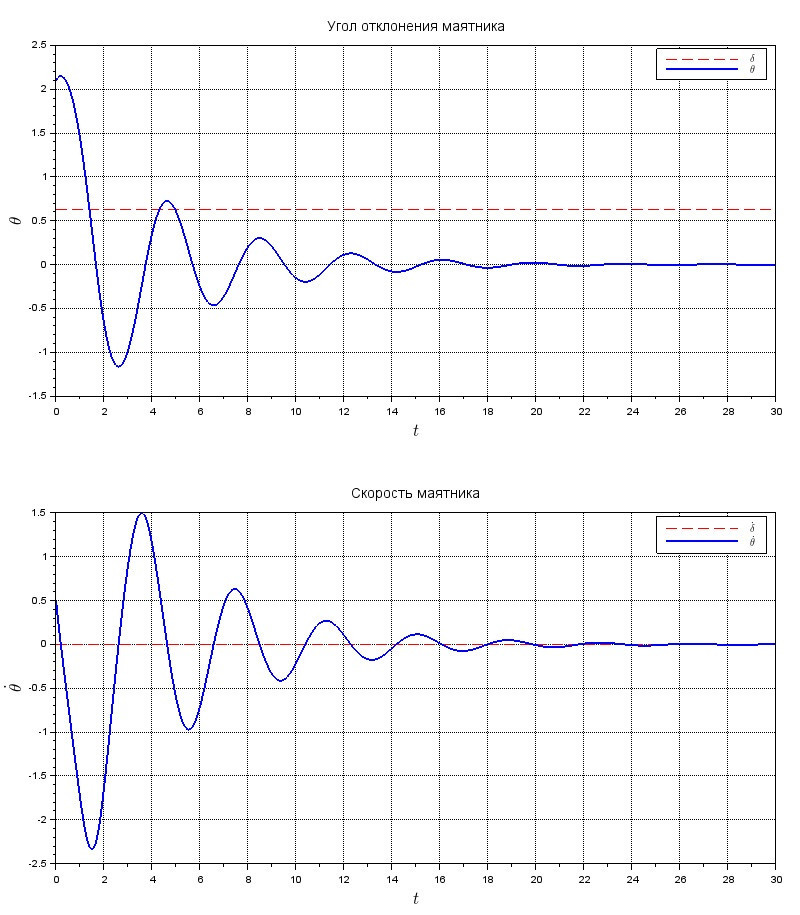
При этом, без управления маятник будет бултыхаться довольно долго и остановится в устойчивом положении равновесия (0,0):
...
U = 0;
...
Создание анимации движения в Scilab
Пойдём дальше и приступим к реализации движущегося объекта.
Для начала, повернём сетку координат на 90 градусов, чтобы маятник смотрела вниз :)
X_r = X - %pi/2;
delta_r = delta- %pi/2;
Добавим звёздочки на координатную сетку - начальное положение и программную позицию маятника
plot(L*cos(X_r(1,1)), L*sin(X_r(1,1)), 'b*');
plot(L*cos(delta_r), L*sin(delta_r), 'r*');
legend('начальное положение', "программная позиция");
xtitle('Математический маятник');
xgrid;
И изобразим маятник в исходном положении с помощью ломаной линии с координатами \( (0, 0) - ( L*cos(X_r(1,1)), L*sin(X_r(1,1)) ) \):
x_ = [0; L*cos(X_r(1,1))];
y_ = [0; L*sin(X_r(1,1))];
xpoly(x_, y_, "lines", 0);
Далее отредактируем параметры элемента xpoly(). Наличие соединений mark имитирует груз на конце стержня маятника, mark_style = 9 говорит, что это кружочек, а mark_offset = 1 отвечает за смещение кружочка относительно линии:
pendulum = gce();
pendulum.foreground = 1;
pendulum.thickness = 2;
pendulum.mark_style = 9;
pendulum.mark_offset = 1;
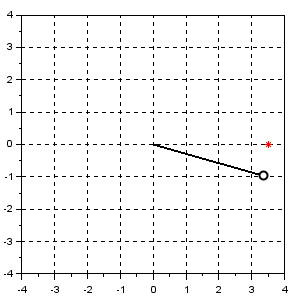
Приступим к имитации движения маятника. Его траектория - это решени системы ОДУ, т.е. элементы матрицы X_r. В первой строке этой матрицы содержится координата маятника \( X_1 = \theta \) в момент времени \( i \), а во второй строке - скорость маятника \( X_2 = \dot\theta \) в этот момент времени. Нам нужна координата для изменения позиции палочки с кружком, причём, центр маятника так и будет оставаться в положении \( (0,0) \), двигаться же будет его не закреплённый конец:
i = 1;
while i<=length(t)
drawlater();
sca(pendulum_axes);
x_ = [0; L*cos(X_r(1,i))];
y_ = [0; L*sin(X_r(1,i))];
pendulum.data = [x_, y_];
drawnow();
i = i + 12;
end
Под действием выбранного управления, маятник быстренько стабилизируется и не бултыхается безумно:
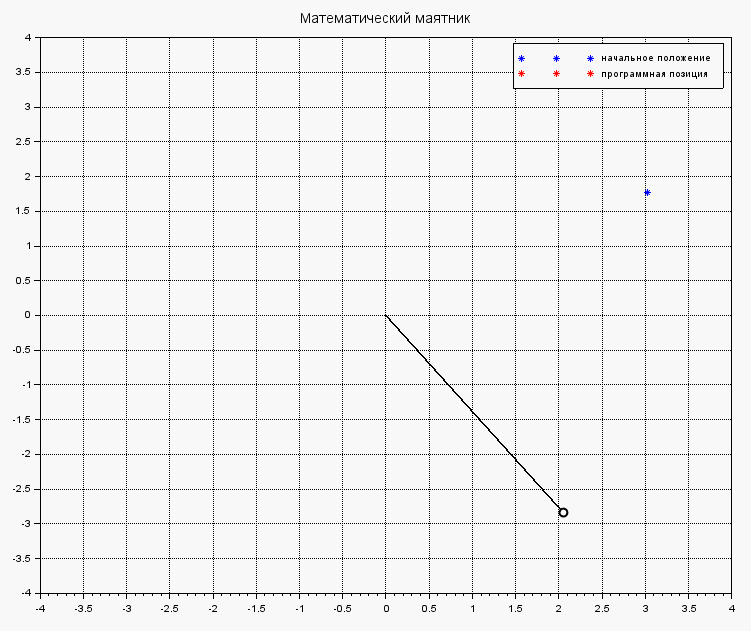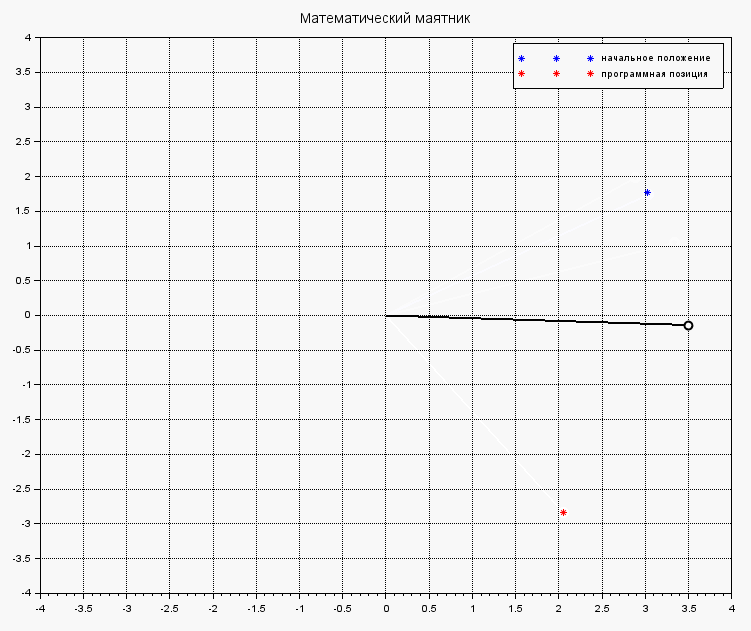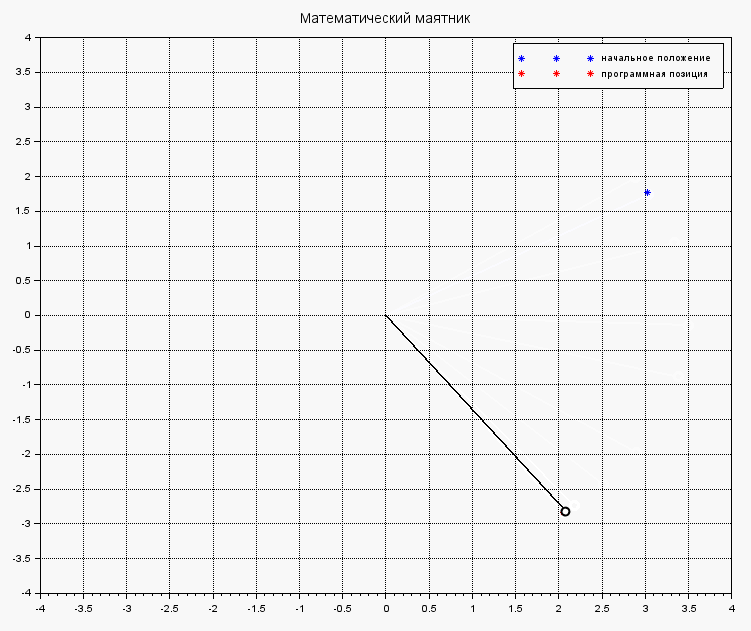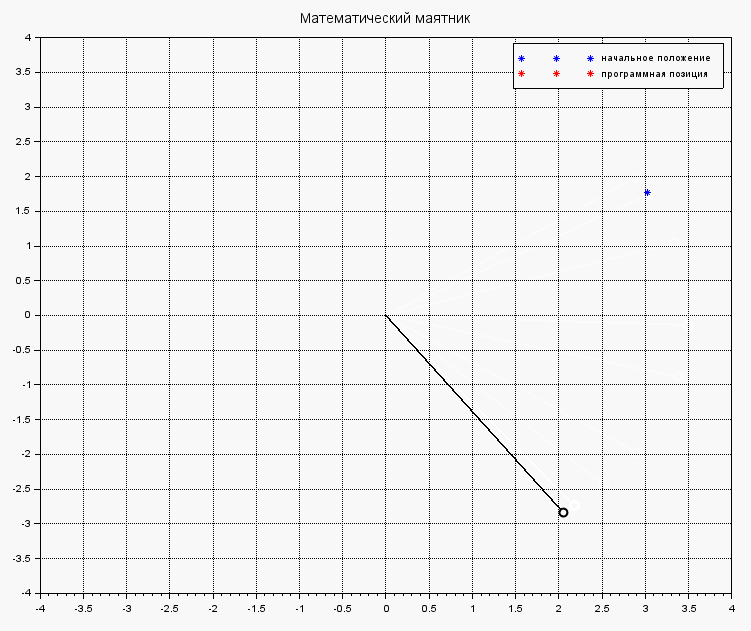
Если же в теле функции systNelin() исключить найденное управление из процеса стабилизации маятника, получим поведения объекта под действием на него исходных внешних сил:
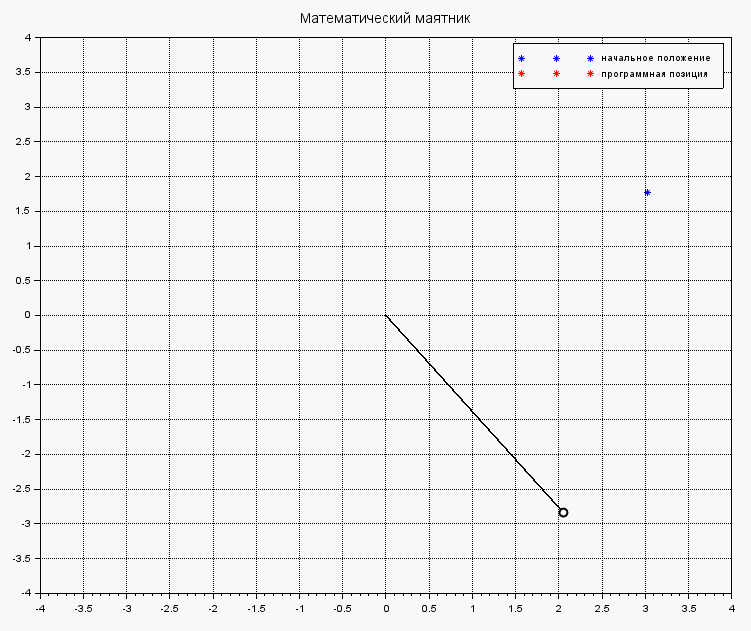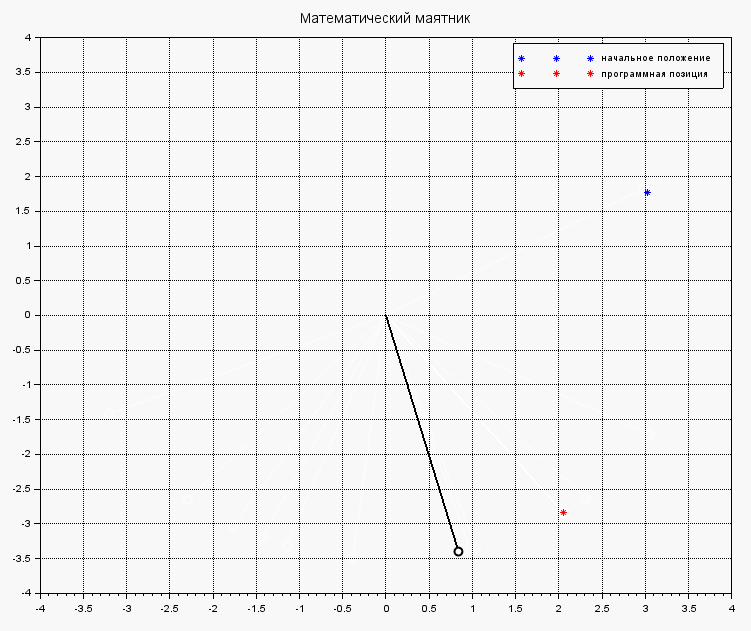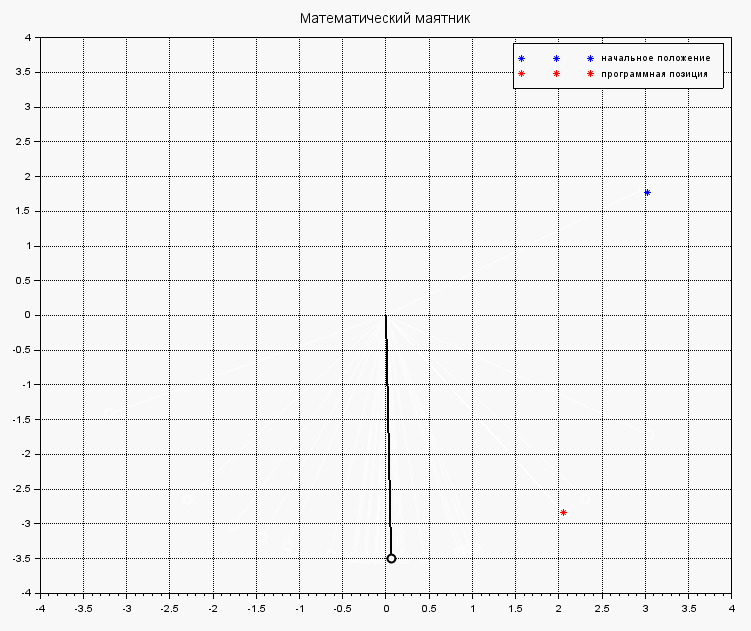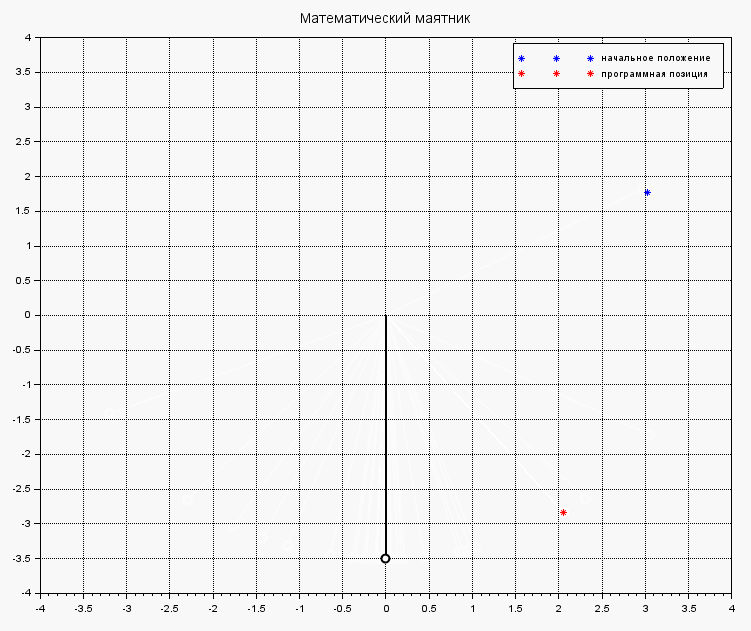

Комментарии