Динамическая вероятностная модель взаимодействия САЗ ИС

Непрерывная цепь Маркова

При моделировании информационных систем часто встречаются ситуации, которые указать заранее невозможно. Например, любая деталь или агрегат могут выходить из строя в любой, непредсказуемый заранее момент времени.

В данной ситуации не удастся обойтись детерминированной матрицей переходов, как в дискретном случае ведь вероятность $p_{i}$ оказаться в состоянии $S_i$ будет функцией времени, то есть:

$p_{i}(t) = p(S_i(t)) \quad i = 1,...,n, \quad t \geq 0 $

Более того, вместо вероятности перехода $p_{ij}$, мы теперь будем говорить о плотности вероятности перехода $\lambda_{ij}(t)$ из состояния $S_i$ в состояние $S_j$ в момент времени t:

$ \lambda_{ij}(t) = \displaystyle\lim_{\Delta t \to 0} \frac{p_{ij}(t,\Delta t)}{\Delta t} $

которая запросто может становиться больше 1.

Вероятности $\lambda_{ij}(t)$ будут составлять матрицу плотностей вероятностей переходов:

\begin{matrix} \Lambda= { \begin{pmatrix} \lambda_{11}(t) & \lambda_{12}(t) & ... & \lambda_{1n}(t) \\ ... & ... & ... & ... \\ \lambda_{n1}(t) & \lambda_{n2}(t) & ... & \lambda_{nn}(t) \end{pmatrix} \quad (1)} \end{matrix}

Однако, несмотря на то, что всё меняется, некоторые вещи остаются неизменными, но становятся другими :)

В случае с непрерывным временем тоже будет иметь место равенство суммы вероятностей 1, которое будем называть нормировочным условием:

$ \displaystyle\sum_{i=1}^{n} p_{i}(t) = 1, \quad \forall t \geq 0 \quad (2) $

Как же отыскать $p_{i}(t)$, если они в явном виде нигде не заданы?

Здесь на помощь приходят дифференциальные уравнения Колмагорова, которые и помогут найти исходные $p_{i}(t)$.

Итак, вероятности состояний $p_{i}(t)$ - это решение системы дифференциальных уравнений вида:

$ \displaystyle\frac{dp_{i}(t)}{dt} = \displaystyle\sum_{j=1}^{n} \lambda_{ji}(t)\cdot p_{j}(t) - \displaystyle\sum_{j=1}^{n} \lambda_{ij}(t)\cdot p_{i}(t) \quad (3) $

Рассмотрим подробнее, что из себя представляет 1-е уравнение системы (3). Для этого заменим все $ i $ на 1 в (3):

$ \displaystyle\frac{dp_{1}(t)}{dt} = \displaystyle\sum_{j=1}^{n} \lambda_{j1}(t)\cdot p_{j}(t) - \displaystyle\sum_{j=1}^{n} \lambda_{1j}(t)\cdot p_{1}(t) \quad $

Теперь стало понятно, что в сумме с плюсом надо пробежаться по 1-му столбцу матрицы (1), домножив каждый элемент на соответствующую вероятность $p_{j}(t)$,
а в сумме с минусом надо пробежаться по 1-ой строке матрицы (1), домножив каждый элемент на вероятность $ p_{1}(t) $.

Если перевести последнее высказывание на язык графов, то получим, что:
производная вероятности 1-го состояния - это сумма произведений входящих стрелок на интенсивности соответствующих потоков
минус сумма произведений исходящих стрелок на интенсивность 1-го потока.

Отсюда можно вывести правило составлений уранений Колмагорова:

В левой части каждого из них стоит производная вероятности i-го состояния.
В правой части
с плюсом - суммарная интенсивность всех потоков, приводящих систему в данное состояние:
с минусом - суммарная интенсивность всех потоков, выводящих систему из данного состояния.

Финальные вероятности

Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени. Особый интерес представляют вероятности системы в предельном стационарном режиме, т.е. при $ t \to \infty $, которые называются предельными (или финальными) вероятностями состояний.

Финальные вероятности состояний находятся путем решения СЛАУ, которые получаются из дифференциальных уравнений Колмогорова (3), если приравнять производные к нулю, а вероятностные функции состояний $ p_1(t),..., p_n(t) $ в правых частях уравнений заменить соответственно на неизвестные финальные вероятности $ p_1^*(t),..., p_n^*(t) $ и добавить нормировочное условие (2).

$ \begin{cases} 0 = \displaystyle\sum_{j=1}^{n} \lambda_{ji}(t)\cdot p^*_{j} - \displaystyle\sum_{j=1}^{n} \lambda_{ij}(t)\cdot p^*_{i} \quad \\ \displaystyle\sum_{i=1}^{n} p^*_{i} = 1 \end{cases} $

Модель взаимодействия копмонент ПО средств активной защиты

Рассмотрим процесс активной защиты информационной компьютерной системы, в которой функционируют 5 комплексов программ.

Пусть плотности вероятности $\lambda_{ij}$ описывают интенсивность передачи управления от $i$-го компекса ПО к $j$-му в процессе решения задач активной защиты КС.

Предположим, что $\lambda_{ij}$ задаются в виде:

$ \lambda_{12} = \frac{1}{T_1}; \lambda_{21} = \frac{1-\alpha}{T_2}; \lambda_{23} = \frac{\alpha}{T_2}; \lambda_{34} = \frac{1}{T_3}; $
$ \lambda_{43} = \frac{1-\beta}{T_4}; \lambda_{45} = \frac{\beta}{T_4}; \lambda_{51} = \frac{1}{T_5}; $

где $\alpha$ - вероятность того, что вторжение злоумышленника бедут распознано САЗ,
$\beta$ - вероятность того, что выявленная уязвимость в КС будет использована для ответных атак.

Через $ p_i(t) $ зададим вероятность того, что в момент времени $ t$ в КС выполняется $i$-й компекс программ.

Пусть взаимодействие комплексов ПО в КС описывается с помощью графа на рис.1

Рисунок 1. Граф связи комплексов ПО в КС.

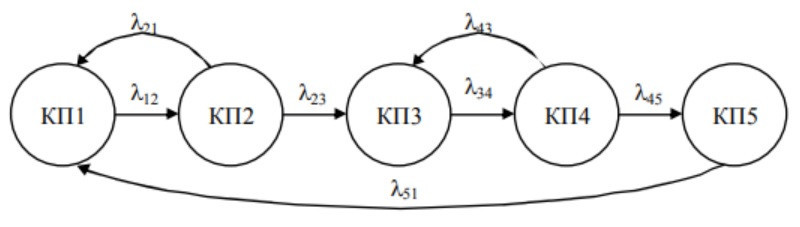
Тогда соответствующая система ДУ Колмагорова будет иметь вид:

$ \begin{cases} \dot p_1 = -\lambda_{12}p_1 + \lambda_{21}p_2 + \lambda_{51}p_5 \\ \dot p_2 = \lambda_{12}p_1 - (\lambda_{21} + \lambda_{23})p_2 \\ \dot p_3 = \lambda_{23}p_2 - \lambda_{34}p_3 + \lambda_{43}p_4 \\ \dot p_4 = \lambda_{34}p_3 - (\lambda_{43} + \lambda_{45})p_4 \\ \dot p_5 = \lambda_{45}p_4 - \lambda_{51}p_5 \end{cases} (4) $

Для того, чтобы с уравнениями Колмагорова было удобнее работать в Scilab, перепишем систему (4) в матричном виде:

\begin{matrix} \dot p = { \begin{pmatrix} -\lambda_{12} & \lambda_{21} & 0 & 0 & \lambda_{51}\\ \lambda_{12} & -(\lambda_{21} + \lambda_{23}) & 0 & 0 & 0\\ 0 & \lambda_{23} & -\lambda_{34} & \lambda_{43} & 0\\ 0 & 0 & \lambda_{34} & - (\lambda_{43} + \lambda_{45}) & 0\\ 0 & 0 & 0 & \lambda_{45} & -\lambda_{51}\\ \end{pmatrix} }p \quad (5) \end{matrix}

Кратко:

$ \dot p = Bp $

Зададим начальные условия для системы (5), т.е. вектор начального состояния (6):

$ p_0 = (1, 0, 0, 0, 0) \quad (6) $

Решение ДУ Колмагорова в Scilab

Решим задачу Коши для системы (5), с н.у. (6) в Scilab.

Решение данной задачи почти не отличается от рассмотренных ранее двумерных систем.

Единственное нововведение - это замена в матрице системы (5) одной из строк на нормировочное условие (2). Это необходимо сделать, т.к. пара уравнений в (5) являются линейно зависимыми.


clc; clf;
function dp = kolm(t, p)
  	// заменим первую строку на условие нормировки
    p(1) = 1 - (p(2) + p(3) + p(4) + p(5));
    dp = B*p;    
endfunction

// зададим параметры системы
T1 = 12;
T2 = 8;
T3 = 20;
T4 = 15;
T5 = 5;

alp = .8;
bet = .7;

a12 = 1/T1;
a21 = (1-alp)/T2;
a23 = alp/T2;
a34 = 1/T3;
a43 = (1 - bet)/T4;
a45 = bet/T4;
a51 = 1/T5;

// сформируем матрицу системы (5)   
B = [-a12, a21, 0, 0, a51; a12, -(a21+a23), 0 0 0; 0, a23, -a34, a43, 0; 0, 0, a34, -(a43+a45), 0; 0, 0, 0, a45, -a51];
n = size(B,1);

// отрезок интегрирования 
t = 0:.1:100;
// начальные условия (6)
p0 = [1; 0; 0; 0; 0];

// решаем дифур
Pt = ode(p0, 0, t, kolm);
plot(t, Pt); 
gce().children.thickness = 4;
xgrid; 
xtitle("Функции распределения вероятностей", "t", "Pj(t)");

Решение ДУ Колмагорова для марковской цепи.

На рис.2 представлены интегральне кривые системы (5), которые и представляют собой вероятности состояний КС как функции времени.

Рисунок 2.Решение ДУ Колмагорова.

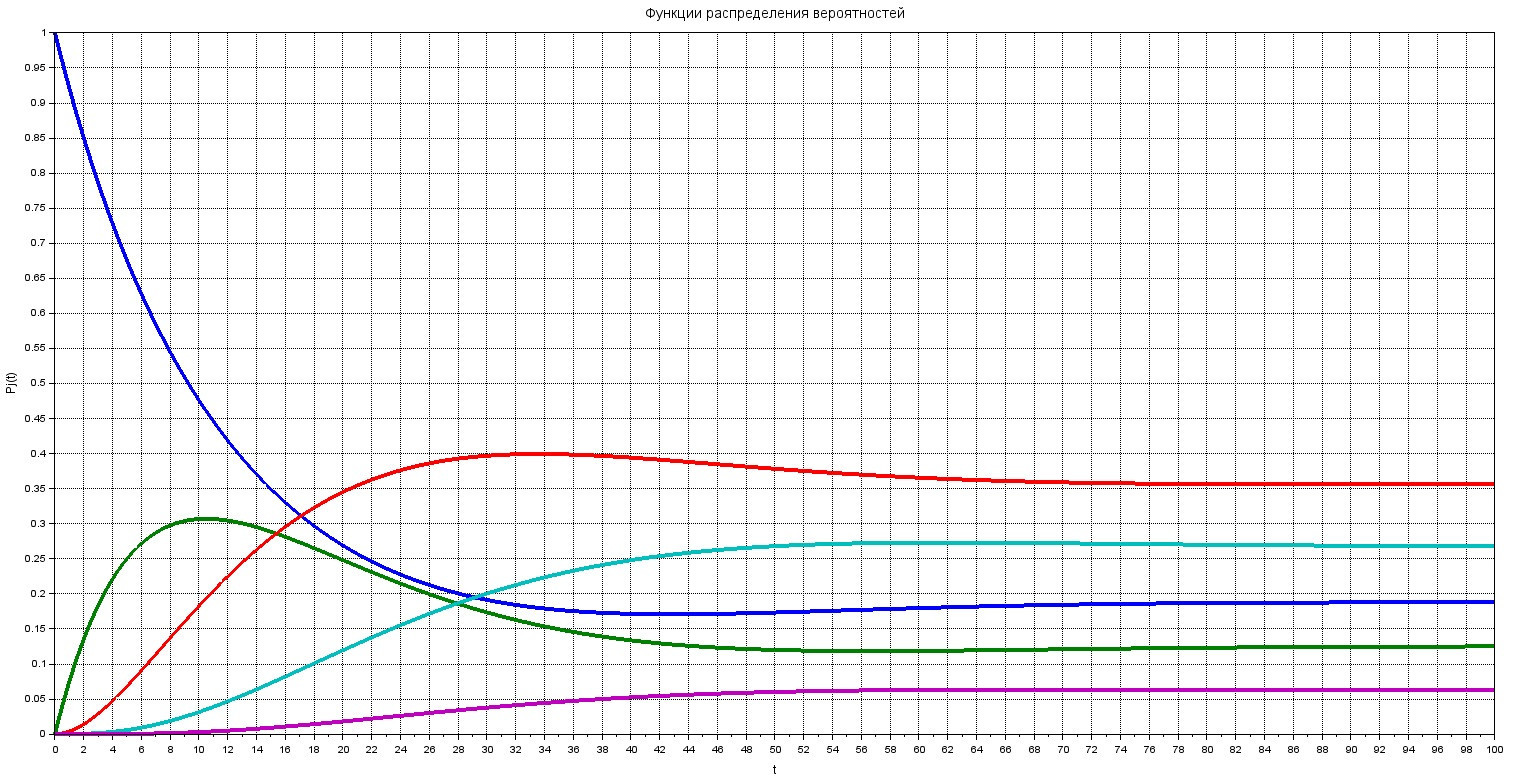
Решение СЛАУ Колмагорова в Scilab

Так как марковский процесс, описывающий взаимодействие компонент ПО САЗ не имеет поглощающих состояний (см. рис.1), то с некоторого момента времени все компоненты КС будут функционировать в стационарном режиме, достигнув финальных вероятностей.

Найдём финальные вероятности $ p_i^* $. Для этого в системе (5) приравняем производные к нулю и решим СЛАУ с условием нормировки (2):

$ \begin{cases} 0 = { \begin{pmatrix} -\lambda_{12} & \lambda_{21} & 0 & 0 & \lambda_{51}\\ \lambda_{12} & -(\lambda_{21} + \lambda_{23}) & 0 & 0 & 0\\ 0 & \lambda_{23} & -\lambda_{34} & \lambda_{43} & 0\\ 0 & 0 & \lambda_{34} & - (\lambda_{43} + \lambda_{45}) & 0\\ 0 & 0 & 0 & \lambda_{45} & -\lambda_{51}\\ \end{pmatrix} }p^* \\ 1 = p_1^* +p_2^* + p_3^* + p_4^* + p_5^* \quad \end{cases} (7) $

Чтобы не запутаться в последовательности линейных преобразований в системе (7), поручим эти действия Scilab.

Прежде всего, приведём матрицу B к ступенчатому виду. Для этого в Scilab имется функция rref:


rB = rref(B);
disp('Приведённая к ступенчатому виду матрица В', rB);

Функция приведения матрицы к ступенчатому виду в Scilab.

Убедимся, что rB действительно ступенчатая да ещё и с одной нулевой строкой (вспомните про ЛЗ уравнений в (5) ) :

Рисунок 3.Ступенчатый вид матрицы В.

Далее нам необходимо заменить последнюю строку матрицы на условие нормировки (2). Это условие выражено 6-м уравнением в системе (7). В нём фигурируют все элементы вектора p с коэффициентами 1. Поэтому последняя строка ступенчатой матрицы превратится в строку единиц.
Последнюю строку матрицы в Scilab можно отыскать с помощью символа $


rB($, :) = ones(n);
disp('Заменим последнюю строку на условие нормировки в матрице В', rB);

Заменим последнюю строку на условие нормировки в матрице В.

Рисунок 4.Ступенчатая матрица со строкой из 1.

Осталось лишь численно решить систему алгебраических уравнений.
В Scilab для решения системы линейных уравнений припасена функция linsolve(A, b), которая ищет вектор x в системе уравнений вида:

$ A*x + b = 0 $

В нашем случае первый аргумемнт функции linsolve(*, *) - это матрица rB, а второй аргумент - это вектор f, сформированный из неоднородностей системы (7), перенесённых за знак "=".


//Вектор f состоит из нулей (левые части ДУ)
f = zeros(n,1);
  
// и последней -1 из нормировочного условия
f($+1) = -1;
disp('Вектор f', f);

// linsolve ищет решение для системы rB*p + f = 0.
Plin = linsolve(B, f);
disp('Численное решенеие системы алгебраических уравнений', Plin)

Численное решенеие системы алгебраических уравнений в Scilab.

Нарисуем финальные вероятности $ p_i^* $, чтобы убедиться, что именно к ним сходится решение ДУ Колмагорова:


colors = ['c--'; 'g--'; 'm--'; 'y--'; 'bl--'];
for i=1:n
    plot( t, t*0 + Plin(i), colors(i) );
    gce().children.thickness = 2;
end

нарисуем вероятности p*.

Рисунок 5.Выход на финальные вероятности интегральных кривых.

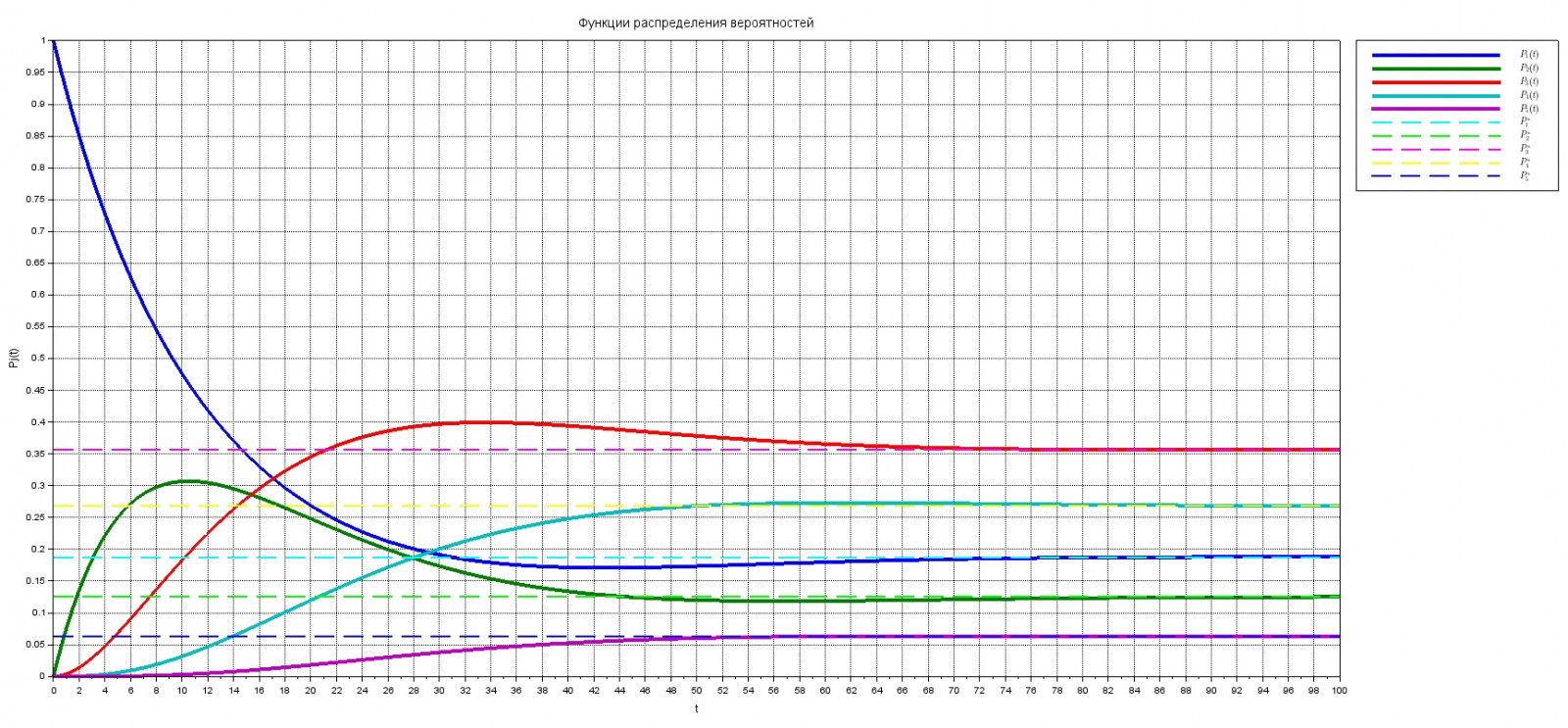
Итак, где-то с 90сек. ПО в системе активной защиты КС будет функционировать в установившемся режиме.

Нравится 22 (лайкай без регистрации)