Комплéксный ряд Фурье и эффект Гиббса
Сгенерируем прямоугольный импульс с заданными характеристиками, построим его спектр и попробуем его восстановить по нескольким гармоникам.
Построение прямоугольного импульса
Прежде всего, напишем функцию, которая будет генерировать несимметричный прямоугольный импульс с заданными характеристиками, например, такой:
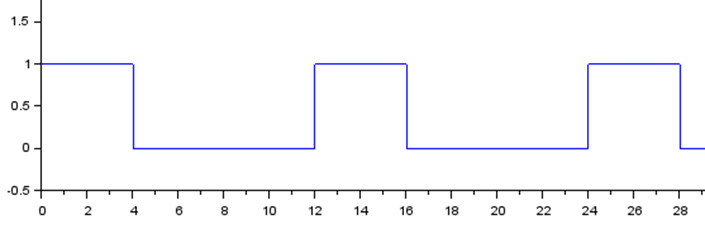
Зададим период и длительность импульса, а также временной промежуток, на котором будем строить импульс:
impPeriod = 12; // период импульсов
impDuration = 4; //длительность импульса
t = 0:.01:3*impPeriod; //временной промежуток
Далее напишем функцию, которая будет строить импульс на заданном промежутке:
function imp_ = imp(t, tau, T)
imp_ = zeros(t);
for k = 1:length(t)
if (modulo( t(k),T) <= tau) then
imp_(k) = 1;
end
end
endfunction
В функции \( imp() \) сначала формируется вектор, заполненный нулями той же размерности, что и временной промежуток.
Чтобы построить прямоугольный импульс, нам нужно на первых 4-х секундах задать его высоту = 1, оставив остальные элементы вектора без изменения (потому что они уже нулевые), а далее повторить эту процедуру с заданным периодом, т.е. через каждые 12 с.
Повторение импульса обеспечивает деление по модулю, которое в Scilab реализовано функцией \( modulo( \cdot, \cdot) \)
Осталось лишь вызвать функцию \( imp() \) с заданными параметрами импульса и немного подкорректировать первый и последний элементы сформированного вектора:
square = imp(t, impDuration, impPeriod);
square(1) = 0; // первый элемент массива в Scilab
square($) = 0; // последний элемент массива в Scilab
Построим график нашей функции, чтобы убедиться, что всё идёт по плану:
subplot(311)
plot(t, square)
gca().data_bounds=[-1,-1;3*impPeriod,1.1];
strtitle = 'несимметричный импульс период=' + string(impPeriod) + ', длительность=' + string(impDuration);
xtitle(strtitle, 't', 'x(t)'); xgrid;
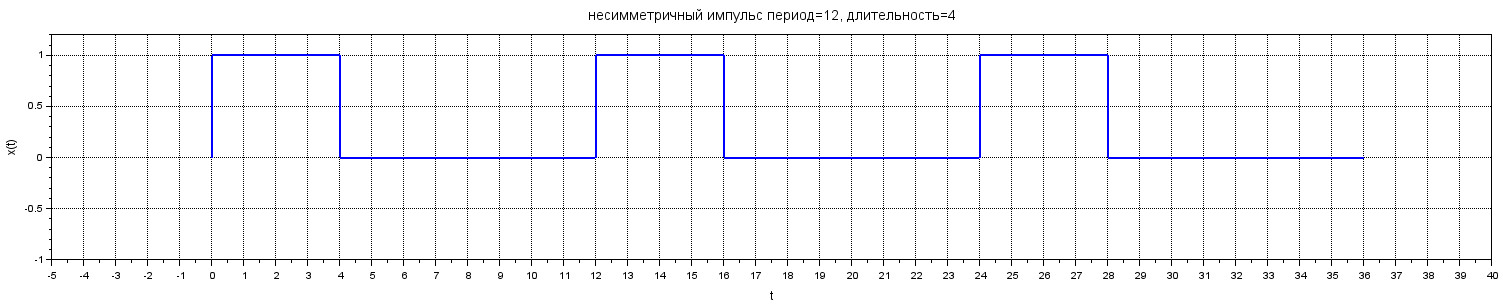
Заметьте, что здесь заголовок графика формируется с учетом заданных характеристик, которые переводятся в строку функцией \( string() \).
Разложение несимметричного импульса в комплексный ряд Фурье
Для несимметричного импульса с амплитудой 1 комплексные коэффициенты Фурье примут вид:
\( c_k = \displaystyle\frac{1}{T} \displaystyle\int_{0}^{\tau} e^{-i\frac{2\pi k t}{T}}dt = \left( \frac{1}{\pi k} sin \left( \frac{\pi k \tau}{T} \right) \right) e^{-i\frac{\pi k \tau}{T}} \quad (1) \)
При этом, на нулевой частоте было деление на 0, поэтому её нужно задать отдельно в виде:
\( c_0 = \displaystyle\frac{\tau}{T} \)
Вычислим коэффициенты \( c_k \) разложения несимметричного импульса в Scilab по формуле (1), заодно посчитаем частоты гармоник \( \omega_k \).
N = 15; //количество гармоник
C = [];
W = [];
C(1) = impDuration/impPeriod;
W(1) = 0;
for k = 1:N
C(k+1) = 1/(%pi*k) * sin(%pi*k*impDuration/T) * exp(-%i*%pi*k*impDuration/impPeriod);
W(k+1) = 2*%pi*k/impPeriod;
end
Выделяем амплитудный и фазовый спектр
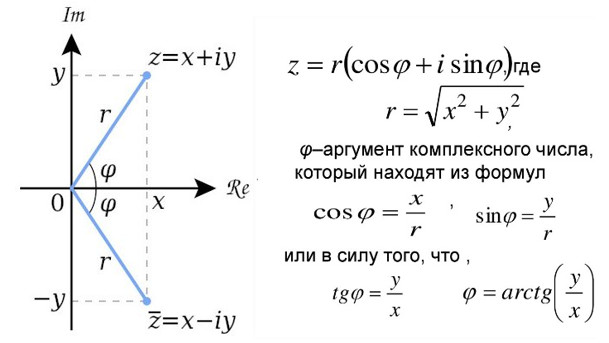
Вещественные коэффициенты \( A_k \) и \( \phi_k \), где
\( A_k = |c_k| \quad \phi_k = arg(c_k) \)
несут полную информацию о периодической с известным периодом \( T \) функции.
Набор \( A_k \) называется амплитудным спектром, а коэффициенты \( \phi_k \) определяют фазы отдельных гармоник, их совокупность называется фазовым спектром.
Из сформированных комплекснозначных коэффициетов Фурье \( c_k \) выделим амплитудный и фазовый спект в Scilab: для нахождения модуля комплексного числа воспользуемся функцией \( abs() \), а угол \( \phi_k \) найдём с помощью функции \( atan(\cdot, \cdot) \).
// выделяем амплитудный и фазовый спектр
Asp = abs(C); //амплитудный спектр
Phasesp = atan(imag(C),real(C)); // фазовый спектр
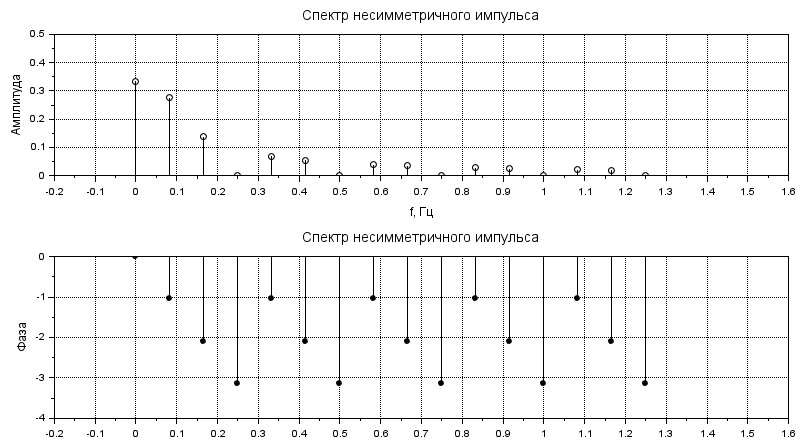
Построим графики найденных спектров. Здесь стоит отметить, что \( A_k \) и \( \phi_k \) - это дискретные величины. Чтобы построить дискретный график в Scilab воспользуемся функцией \( plot2d3() \) в совокупности с классическим \( plot() \), который будет формировать кружочки:
subplot(312);
xtitle('Спектр несимметричного импульса', 'f, Гц', 'Амплитуда'); xgrid;
plot(W/2/%pi, Asp, 'ko');
plot2d3(W/2/%pi, Asp);
gca().data_bounds=[-.1,0;1.5,0.5];
subplot(313);
xtitle('Спектр несимметричного импульса', 'f, Гц', 'Фаза'); xgrid;
plot(W/2/%pi, Phasesp, 'k.');
plot2d3(W/2/%pi, Phasesp);
gca().data_bounds=[-.1,-4;1.5,0];
Восстанавливаем несимметричный импульс
Периодическая функция, представленная в виде комплексного ряда Фурье, может быть восстановлена по найденным коэффициентам (1) согласно формуле:
\( x(t) = c_0 + 2 \displaystyle \sum_{k=1}^{+\infty} |c_k| cos(\omega_k t + arg(c_k)) \quad (2) \)
Представим формулу (2) на языке Scilab. Чтобы процесс был более наглядным, выражение под знаком суммы в (2) вынесем в отдельную функцию, аргументами которой будут: модуль комлекных коэффициентов \( |c_k| \) , частоты гармоник \( \omega_k \), временной промежуток - транспонированный вектор \( t \) и аргумент комлекных коэффициентов \( arg(c_k) \):
signal = C(1) + 2*summ(abs(C), W, t', atan(imag(C),real(C)));
Заметьте, что коэффициент \( |c_0| \) представлен как \( С(1) \), так как нумерация элементов массива в Scilab начинается с 1.
Функция \( summ() \) будет иметь следующий вид:
function s_ = summ(modC, W, t, argC)
s_ = zeros(length(t));
for k = 2:N+1
s_ = s_ + modC(k) * cos(W(k)*t + argC(k));
end
endfunction
Итак, осталось лишь вывести восстановленный сигнал и посмотреть, насколько он совпадает с оригинальным:
subplot(311);
plot(t, signal, 'r-');
legend('Исходный сигнал', "Восстановленный сигнал", 4);

На графике можно заметить осцилляции в точках излома импульса.
Если взять число гармоник \( N=50\), то картина улучшится, но кардинально не изменится:
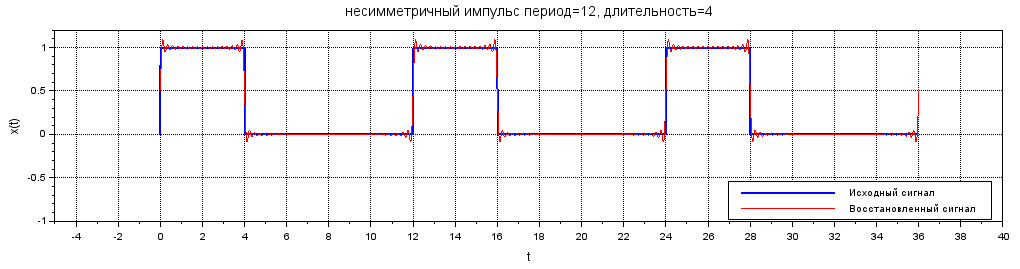
Дело в том, что если функция, которую раскладывают в ряд Фурье, имеет разрывы первого рода, то в точках разрыва ряд сходится к полусумме значений функции слева и справа от точки разрыва. Если оставить в сумме конечное число слагаемых, то есть выполнять приближение функции тригонометрическим полиномом, то в окрестности точки разрыва будут осцилляции. Это называется эффектом Гиббса.

Комментарии