Модель 3-х популяций в среде Xcos
Рассмотрим простейшую модель распространения болезни в обществе. Обозначим через \( s(t) \) - долю особей, потенциально подверженных заболеванию, \( i(t) \) - долю уже заболевших (и потенциально заразных) особей, а через \( r(t) \) - число выздоровевших и, следовательно, приобрётших иммунитет к болезни. В данных обозначениях математическая модель течения болезни в трёх взаимодействующих популяциях представима в виде:
(1)\begin{cases} \dot{s}=-as(t)i(t) \\ \dot{i}=as(t)i(t)-bi(t) \\ \dot{r}=bi(t) \end{cases}
\( a>0, b>0 \)
Создание блок-схемы, описывающей взаимодействие трёх популяций, как и в предыдущем случае, начнём с задания положительных коэффициентов \( a=1, b=0.3 \) через контекст. Кроме того, зададим начальные значения \( s_0=0.999, i_0=0.001 \), обозначающие долю особей, восприимчивых и не восприимчивых к болезни соответственно.
Далее добавим на рабочую область три блока интегратора INTEGRAL_m с настроенными внутренними параметрами, один блок сумматора BIGSOM_f и два блока усилителя GAINBLK с параметрами \( a,b \).
В итоге получим заготовку, изображённую на рис. 51.
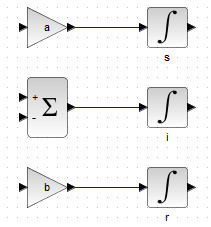
Далее замоделируем правую часть уравнения \( \dot{s}=-as(t)i(t) \) как произведение двух фазовых переменных, усиленное на величину \( -a \).
В результате получим схему, изображенную на рис. 52
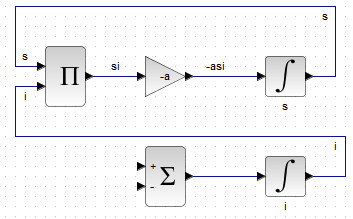
Соединительные линии для второго и третьего уравнений проводятся по известным уже принципам умножения фазовых переменных с помощью блока PRODUCT и их последующего усиления через блок GAINBLK.
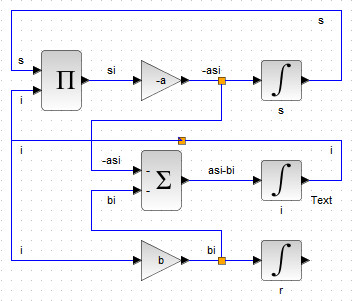
Интересным в рассматриваемом примере является второе уравнение \( \dot{i}=as(t)i(t)-bi(t) \) рассматриваемой системы (1). Дело в том, что оба слагаемых, стоящих в правой части данного уравнения, входят в состав первого и третьего уравнений с теми же коэффициентами усиления, но противоположными знаками. Поэтому добавлять дополнительные блоки усилителей не нужно, достаточно распараллелить соответствующие соединительные линии блоков и отредактировать знаки слагаемых блока BIGSOM_f , как показано на рис. 53.
Для вывода графического решения рассматриваемой системы трёх взаимодействующих популяций, воспользуемся приёмом, рассмотренным в предыдущей статье. Добавим блоки TOWS_c, CLOCK_c, END, проведя соединительные линии и настроив их внутренние параметры для моделирования на протяжении 20сек., как показано на рис. 54.
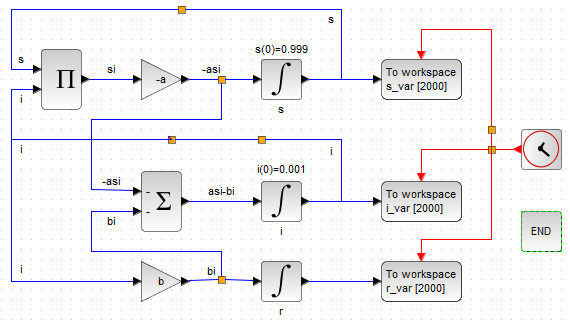
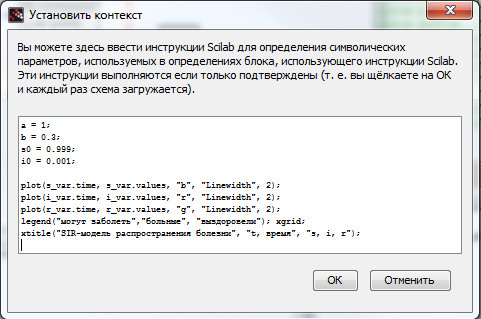
Далее необходимо установить контекст, как показано на рис. 55.
Результаты моделирования представлены на рис. 56. Моделирование проводилось для с шагом дискретизации 0.1.
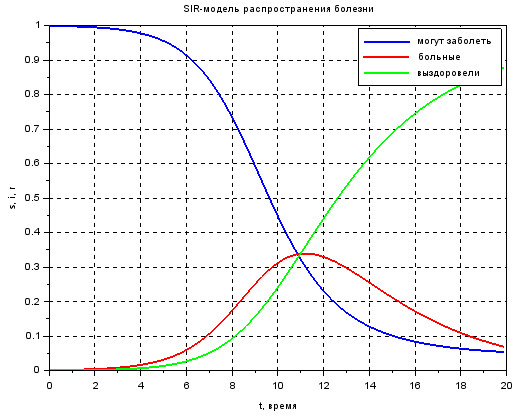
На основе результатов моделирования, можно сделать вывод, что доля переболевших и приобретших иммунитет особей, растёт со временем, в то время, как число потенциально подверженных заболеванию падает. Процент заражённых особей сначала возрастает, достигая своего максимума в точке, называемой «пиком эпидемии», а далее снижается, стремясь к нулю.

Комментарии