построение дискретного наблюдателя в СДУ в Xcos
Итак, на данный момент читатель последовательно прошёл путь от создания простейшей блок-схемы Xcos, состоящей всего из трёх блоков, до визуального моделирования полноценных управляемых динамических систем, описываемых матричными уравнениями.
В настоящем параграфе будет затронута ещё одна задача математического моделирования – построение дискретного наблюдателя в системе дифференциальных матричных уравнений.
Данная задача особенно актуальна, так как при моделировании управляющего воздействия динамической системы, как бы удобно ни было управлять состоянием \( x\), его измерение, чаще всего не доступно. Поэтому на практике для управляемых динамических систем строится специальный наблюдатель \( y\), который сам по себе представляет динамическую систему.
Построение непрерывного наблюдателя
Построение системы наблюдения происходит так, чтобы на вход наблюдателя подавались значения \( u,y\), а на выходе формировался бы сигнал \( \hat{x} \). При этом, матрицы системы наблюдения должны быть подобраны таким образом, чтобы разность \( x-\hat{x} \) стремилась бы к нулю не зависимо от выбранных начальных условий или самого вида наблюдателя. Отличительной особенностью наблюдателей такого рода, является устойчивость к возмущениям.
Отметим также, что при выборе коэффициентов усиления наблюдателя необходимо поддерживать баланс между скоростью и точностью сходимости моделируемого движения к программному и чрезмерной чувствительностью к начальным отклонениям.
Рассмотрим пример построения линейного наблюдателя для динамической системы, описываемой в пространстве состояний матричными дифференциальными уравнениями вида:
(1) \[ \begin{cases} \dot x = Ax+Bu\\ \dot y = Cx\\ \end{cases} \]
где \(A, B, C\) - матрицы с постоянными коэффициентами.
Непрерывный наблюдатель в данном случае, строится следующим образом:
(2) \[ \dot{\hat{x}} = A\hat{x}+Bu+K(y-C\hat{x})\]
при этом, элементы матрицы усиления \( K \) выбираются так, чтобы матрица \( H=A-KC \) была бы устойчивой, то есть, все собственные значения матрицы \( H \) должны иметь отрицательные действительные части.
Построение матрицы \( H \) становится очевидным, если в (1) раскрыть скобки:
\[ \dot{\hat{x}} = A\hat{x}+Bu+Ky-KC\hat{x} = (A-KC)\hat{x} + Bu + Ky \]
Далее определнмся, почему требование устойчивости матрицы \( H \) обеспечивает сходимость к нулю разности \( x-\hat{x} \) .
Введём обозначение \( \widetilde{x} = x-\hat{x} \), тогда \( \dot{\widetilde{x}} = \dot{x}-\dot{\hat{x}} \). Из системы (1) имеем:
\[ \dot{x} = Ax+Bu, y=Cx \]
В уравнении (2), раскрывая скобки, получим:
\[ \dot{\hat{x}} = A\hat{x}+Bu+Ky-KC\hat{x} \]
Теперь вычислим \( \dot{\widetilde{x}} \) :
\[ \dot{\widetilde{x}} = \dot{x}-\dot{\hat{x}} = Ax+Bu - (A\hat{x}+Bu+Ky-KC\hat{x} ) = A - A\hat{x} - Ky + KC\hat{x}= \] \[ = A(x-\hat{x}) - KCx + KC\hat{x}= A(x-\hat{x}) - KC(x-\hat{x}) = (A- KC)\widetilde{x}\]
Таким образом, приходим к однородной системе матричных дифференциальных уравнений с постоянными коэффициентами вида:
\[ \dot{\widetilde{x}} = (A-KC) \widetilde{x}, \quad\quad \text{или} \quad\quad \dot{\widetilde{x}} = H \widetilde{x} \]
об устойчивость решения \( \widetilde{x} \) которой, можно судить по виду корней соответствующего характеристического уравнения \( \chi (\lambda) = |H-\lambda E| \).
Итак, с обоснованием корректности построения описанного непрерывного наблюдателя покончено, перейдём теперь к реализации блок-схемы Xcos.
Для моделирования системы (24) с непрерывным наблюдателем (25) потребуются блоки GENSIN_f и CLOCK_c с палитры «Источники сигналов и воздействий», блоки CSСOPE и END с палитры «Регистрирующие устройства», и блок CLSS с палитры «Системы с непрерывным временем».
Моделирование данной системы подразумевает задание матриц \( A, B, C, D \) , которые используются в блоке CLSS. В нашем случае все элементы матриц некоторые случайные константы, поэтому мы можем их задать в контексте с помощью генератора случайных чисел с некоторыми поправками.
Для начала зададим размерности матрицы в контексте:
clc;
n = 3; m = 1;
и сгенерируем матрицу размерности nxn:
A = rand(n,n)
Для того, чтобы избежать экспоненциальной неустойчивости рассматриваемой системы, изменим матрицу \( A\) так, чтобы каждый из её элементов, стоящих на главной диагонали, не превышал бы собственного значения с максимальной действительной частью \( \widetilde{\lambda} \).
Введём обозначение \( \widetilde{\lambda} = max_{j}{(Re(\lambda_j))} \) , тогда матрица \( \widetilde{A}\) будет вычисляться как \( \widetilde{A} = A- \widetilde{\lambda}E \). В контексте данное равенство реализуется следующим образом:
A = A max(real(spec(A)))*eye();
где функция spec(A) – вычисляет собственные значения матрица , функция real() – выделяет действительную часть своего аргумента, функция max() вычисляет максимальное из поданных в неё значений, а eye() – генерирует единичную матрицу совместной размерности.
Далее сгенерируем матрицы совместных размерностей \( B, C, D \):
B = rand(n, 1); C = rand(m, n); D = zeros(m, 1);
И вектор-столбец \( x^0 \) случайных начальных условий:
X0 = rand(n, 1);
Для генерации матрицы усиления воспользуемся встроенной Scilab – функцией ppol(A,B,v), которая по заданным матрицам \( A,B \) и вектору полюсов \( v \) подбирает элементы матрицы \( K \) так, чтобы собственные значения матрицы \(A-BK\) были бы полюсами.
Однако для нашего наблюдателя должно выполняться то же условие, но для уравнения \( A-KC \), поэтому в контекст необходимо добавить строку:
K = ppol(A',C', -ones(X0))';
где символ «\( ' \) » означает транспонирование матрицы, а функция ones() возвращает матрицу составленную из единиц того же размера, что и вектор \( x^0 \).
Теперь необходимо собрать все сгенерированные матрицы в систему, что делается с помощью функции syslin(dom,A,B,C [,D [,x0] ]), которая генерирует систему вида
\[ \begin{cases} s \cdot x = Ax+Bu\\ y = Cx + Du\\ x(0)=X0\\ \end{cases} \]
соответственно, в контекст необходимо прописать:
SYST = syslin('c', A-K*C, [B,K], eye(A), zeros([B,K]));
После задания в контексте всех необходимых параметров системы, нужно перейти к редактированию внутренних параметров блока CLSS, где необходимо задать правильные матрицы:

Блок схема, реализующая моделирование системы имеет несложный вид:
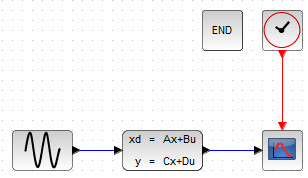
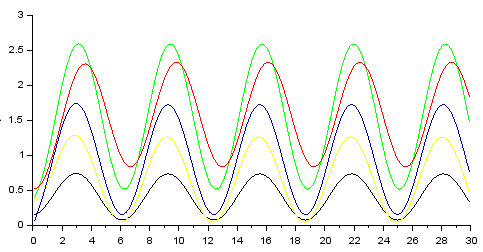
Результат моделирования представлен на рисунке 102(б):
Построение дискретного наблюдателя
В связи с тем, что в параграфе упоминается наблюдатель дискретный, то вполне предсказуемым шагом является модернизация блок-схемы (рис. 102 а)) таким образом, чтобы использовать в ней дискретный наблюдатель.
Построение дискретного наблюдателя подчиняется тем же правилам, что непрерывного, основанных на получении полюсов в качестве собственных значений матрицы \(H = A-KC \).
Поэтому алгоритм, прописанный на данный момент в контексте рабочей области, полностью удовлетворяет нашим требованиям. Остаётся только задать шаг дискретизации и дикретизировать полученную систему \( SYST \) . Для этого добавьте в контекст строки:
dt = 0.2;
SYST_d = dscr(SYST, dt);
[Ad, Bd, Cd, Dd] = abcd(SYST_d);
где Scilab-функция dscr() производит дискретизацию непрерывной системы \( SYST \) с указанным шагом , \( dt \) а встроенная функция abcd() возвращает 4 матрицы \( A,B,C,D \) , использующиеся в поданной на вход дискретной системе и записывает их в соответствующие выходные матрицы \( Ad, Bd, Cd, Dd \) .
В итоге контекст должен принять вид:
clc;
n=3; m=2;
A = rand(n,n); A = A - max(real(spec(A)))*eye();
B = rand(n,1); C = rand(m,n); D = zeros(m,1);
x0 = rand(n, 1);
K = ppol(A',C',-ones(x0))';
SYST = syslin('c', A-K*C, [B,K], eye(A), zeros([B,K]));
dt = 0.2;
SYST_d = dscr(SYST, dt);
[Ad, Bd, Cd, Dd] = abcd(SYST_d);
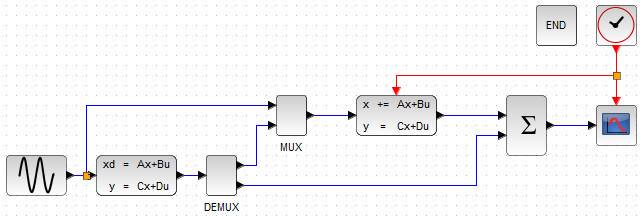
Для внедрения дискретного наблюдателя воспользуемся блоком 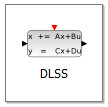 с палитры «Системы с дискретным временем». Кроме того нам понадобятся блоки MUX и DEMUX с палитры «Маршрутизация сигналов» и блок сумматора BIGSOM_f с палитры «Математические операции». Блок-схема реализующая математическое моделирование системы дифференциальных уравнений с дискретным наблюдателем, представлена на рис. 103
с палитры «Системы с дискретным временем». Кроме того нам понадобятся блоки MUX и DEMUX с палитры «Маршрутизация сигналов» и блок сумматора BIGSOM_f с палитры «Математические операции». Блок-схема реализующая математическое моделирование системы дифференциальных уравнений с дискретным наблюдателем, представлена на рис. 103
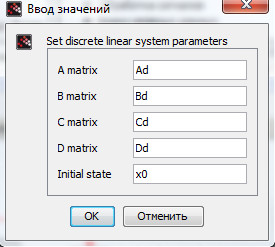
Внутренние параметры блока дискретной линейной системы DLSS представлены на рис. 104
Результат моделирования линейной динамической системы с дискретным наблюдателем представлен на рис. 105.


Комментарии